Пусть n = x, мне просто так удобнее)
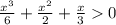
Обе части уравнение умножим на 6:
х³+3х²+2х>0
х(х²+3х+2)>0
х(х+1)(х+2)>0
При любых натуральных значениях х, х(х+1)(х+2) > 0(то есть является натуральным числом)
___________________
2 решение :
Рассмотрим по отдельности каждое слагаемое:
х³/6 > 0 | *6
х³>0
х > 0
То есть х³/6 больше нуля при всех натуральных числах.
____________________________
Если рассмотреть остальные 2 слагаемых, то там будет тоже самое(мне просто лень писать).
____________________________
Если каждое из слагаемых больше нуля, то и сама сумма больше нуля, то есть является натуральным числом)
Сократите дробь:а)(36-а)/(6-√а)=((6-√а)(6+√а))/(6-√а)=(6+√а)
б)(5-√5)/(√15-√3)=(√5(√5-1))/(√3(√5-1))= √(5/3)
освободитесь от знака корня в знаменателе: а)15/√5
15=√5*√5*3,соответственно 15/√5=(√5*√5*3)/√5=3√5
б)5/(√13 - √3) здесь используется метод домножения на сопряженное, соответственно:
5/(√13 - √3) =5(√13 + √3) /(13-3)=(√13 + √3)/2
докажите что значение выражения 4/2√3 - 1 - 4/2√3 - 1 является рациональным числом:
4/2√3 - 1 - 4/2√3 - 1 это выражение равно -2, так как если мы переставим слагаемые по-другому,получим:
4/2√3 - 4/2√3 -1 -1, отсюда видно что:
4/2√3 - 1 - 4/2√3 - 1= -2
упростите выражение а)√х в шестой степени = х^3 так как √х^6= x^(6/2) и соответственно это x^3
(x+4)²-(x-2)(x+2)=х²+2*4х+4²-(х²-2²)=х²+8х+16-х²+4=8х+20 при
x=-0,125 8*(-0,125)+20=-1+20=19
2(3x-2y)(3x+2y)=2((3х)²-(2у)²)=2(9х²-4у²)=18х²-8у²
(a³+b²)²= (а³)² + 2*а³*b²+(b²)²=а в 6 степени+2а³b²+b в 4 степени
(a-5)²-(a+5)²=((а-5)-(а+5))((а-5)+(а+5))=(а-5-а-5)(а-5+а+5)=(-10)(а²)
(2x-5)²-(2x-3)(2x+3)=0
4х²-20х+25-(4х²-9)=0
4х²-20х+25-4х²+9=0
-20х+34=0
-20х=-34
х=(-34):(-20)
х=1,7
9y²-25=0
9у²=25
у²=25\9
у1=5\9 у2=-5\9