1)Координаты точки пересечения прямых (4; 1)
Решение системы уравнений х=4
у=1
2)Система уравнений имеет бесконечное множество решений
3)Система уравнений не имеет решений.
Объяснение:
Решить графически систему уравнений:
1){х+2у=6
{х-4у=0;
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
х+2у=6 х-4у=0
2у=6-х -4у= -х
у=(6-х)/2 4у=х
у=х/4
Таблицы:
х -1 0 1 х -2 0 2
у 3,5 3 2,5 у 0,5 0 0,5
Согласно графика, координаты точки пересечения прямых (4; 1)
Решение системы уравнений х=4
у=1
2){3х+2у=1
{6х+4у=2;
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
3х+2у=1 6х+4у=2
2у=1-3х 4у=2-6х/2
у=(1-3х)/2 2у=1-3х
у=(1-3х)/2
Таблицы:
х -1 0 1 х -1 0 1
у 2 0,5 -1 у 2 0,5 -1
Графики данных функций "сливаются", полностью совпадают, значит, система уравнений имеет бесконечное множество решений.
3){-2х+у=0
{-4х+2у=6
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
-2х+у=0 -4х+2у=6/2
у=2х -2х+у=3
у=3+2х
Таблицы:
х -1 0 1 х -1 0 1
у -2 0 2 у 1 3 5
Графики данных функций параллельны, значит, система уравнений не имеет решений.
Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
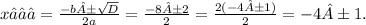
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
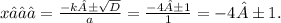
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
y'=(-(x²-x-20)^(-2))*(2x-1)=-(2x-1)/((x+4)(x-5))
2) y=(x-7)/(2x²+5)
y'=(2x²+5-4x(x-7))/(2x²+5)²=(-2x²+28x+5)/(4x^4+20x²+25)