Семиклассник получил за четвёртую четверть по мате- матике ровно 20 оценок и его средний был равен 4,35. после этого было замечено, что в журнал закралась ошибка, и одну из двоек ему исправили на пятёрку. семиклассник в этой четверти со- бирается написать ещё 4 работы, за которые получит ещё 4 оценки. чему должно быть равно среднее арифметическое этих четырёх но- вых оценок для того, чтобы средний по стал равен 4,75? (ответ округлите до сотых).
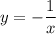и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
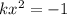и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
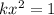и при k<0 это уравнение решений не имеет.
, имеем
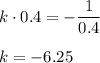
6
Объяснение:
пусть сумма первых 20ти оценок равна х.
тогда их средний 4.35:
х/20=4.35
х=20*4.35=87
при этом одну двойку исправили на пятерку, то есть сумма увеличилась на 3 (с 87 до 90).
пусть средний четырех новых оценок равен k.
(90 + 4*k)/ 24= 4.75
90 + 4*k = 4.75 * 24
90 + 4*k = 114
4*k = 114-90
4*k = 24
k = 24/4=6