Могу предложить несколько корявое, но все же решение... наверное.
Обозначим за a и b цифры искомого числа. Тогда из условия задачи это число есть
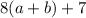и 
приравняем выражения, будем считать a переменной величиной, а b какой-то постоянной, тогда это будет квадратным уравнением относительно a :
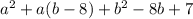
Решая обычным образом находим
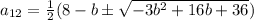
Мы знаем, что a и b - цифры, т.е. они могут быть лишь величинами 0 1 2 3 4 5 6 7 8 9
Смотрим, при самых очевидных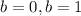 
корень нормально извлекается.
Тогда
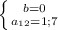
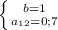
Из всех возможных двузначных чисел (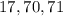
) подходящим оказывается только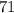 
Подтвердить это можно только непосредственной проверкой
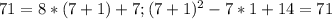
Объяснение:
b₃=b₂+18; b₃=b₁q+18; b₃=b₁q²
b₃=b₁+9; b₃=b₁q²
Система уравнений:
b₁q+18=b₁q²; b₁q²-b₁q=18; b₁q(q-1)=18
b₁+9=b₁q²; b₁q²-b₁=9; b₁(q²-1)=9; b₁(q-1)(q+1)=9
(b₁q(q-1))/(b₁(q-1)(q+1))=18/9
q/(q+1)=2
q=2q+2
q-2q=2
q=-2 - знаменатель геометрической прогрессии.
b₁+9=b₁·(-2)²; b₁+9=4b₁; 9=4b₁-b₁; b₁=9/3=3 - 1-й член геометрической прогрессии.
b₃=3+9=12 - 3-й член геометрической прогрессии.
b₂=12-18=-6 - 2-й член геометрической прогрессии.
b₄=b₃q=12·(-2)=-24 - 4-й член геометрической прогрессии.
b₅=b₄q=-24·(-2)=48 - 5-й член геометрической прогрессии.
(0.6+2x)²=0.6²+2.4+4x²=(6/10)²+2.4x+4x²=(3/5)²+2.4x+4x²=9/25+2.4x+4x²=0.36+2.4x+4x²