х - цифра десятков (0<x<9)
у - цифра единиц (0<y<9)
По условию сумма цифр двузначного числа равна 8, получаем первое уравнение:
х+у=8
(10х+у) - данное число
(10у+х) - число, записанное теми же цифрами, но в обратном порядке.
По условию если данное число разделить на число, записанное теми же цифрами,но в обратном порядке, то в частном получится 4 в остатке 3.
(10х+у) : (10у+х) = 4(ост. 3)
Получим второе уравнение:
10х+у = 4·(10у+х)+3
Упростим его:
10х+у=40у+4х+3
6х-39у = 3
2х-13у = 1
Решаем систему:
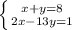
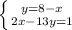

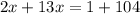
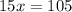
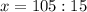
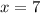

7 - цифра десятков
1 - цифра единиц
71 - данное число
ответ: 71
как всегда с логарифмами ОДЗ и решать неравенство
log(a) b a>0 a≠1 b>0
смотрим и видим что проверять надо только b>0
cначала решим, потом одз найдем и все пересечем
log(1/3) (log(5) ( log(2) (7x - 3)/(x - 4 ≥ 0
log(1/3) (log(5) ( log(2) (7x - 3)/(x - 4 ≥ log(1/3) 1
основание меньше 1, меняем знак при снятии логарифма
log(5) ( log(2) (7x - 3)/(x - 4)) ≤ 1
log(5) ( log(2) (7x - 3)/(x - 4)) ≤ log(5) 5
log(2) (7x - 3)/(x - 4) ≤ 5
log(2) (7x - 3)/(x - 4) ≤ log(2) 2^5
(7x - 3)/(x - 4) - 32 ≤ 0
(7x - 3 - 32x + 128)/(x - 4) = (125 - 25x)/(x - 4) ≤ 0
(x - 5)/(x - 4) ≥ 0
(4) [5]
x ∈ (-∞, 4) U [5, +∞)
ну и пошли одз считать
1. (7x - 3)/(x - 4) > 0
2. log(2) (7x - 3)/(x - 4) > 0
log(2) (7x - 3)/(x - 4) > log(2) 1
(7x - 3)/(x - 4) > 1
3. log(5) ( log(2) (7x - 3)/(x - 4)) > 0
log(5) ( log(2) (7x - 3)/(x - 4)) > log(5) 1
log(2) (7x - 3)/(x - 4) > 1
log(2) (7x - 3)/(x - 4) > log(2) 2
(7x - 3)/(x - 4) > 2
видим что одно значение > 0, 1 и 2
можно каждое посчитать а можно одно большее 2 и оно будет самым обширным
(7x - 3)/(x - 4) - 2 > 0
(7x - 3 - 2x + 8)/(x - 4) > 0
(5x + 5)/(x - 4) > 0
(-1)(4)
x ∈ (-∞, -1) U (4, +∞) пересекаем с x ∈ (-∞, 4) U [5, +∞)
ответ x ∈ (-∞, -1) U [5, +∞)
Предел дроби n/(n+1) = 1 при n, стремящемся к бесконечности.
Если вы понимаете, что такое предел, и как его считать, то это просто.
Поэтому ответ на 1) НЕТ, а на 2) ДА.