ответ: 1) 1; 2) ctg2a
Объяснение:

cos^2 a = 1 - sin^2 a
cos a = ±√ (1 - sin^2 a )
В первой четверти косинус положителен, значит:
cos a = √ (1 - sin^2 a )
cos a = √ (1 - 25/169)
cos a = √ 144/169
cos a = 12/13
Тогда тангенс (отношение синуса к косинусу) равен:
tg a = (5/13)/(12/13) = 5/12
ответ: cos a = 12/13, tg a = 5/12.
2 вариант (если угол альфа расположен во второй четверти) .
Используем основное тригонометрическое тождество:
cos^2 a = 1 - sin^2 a
cos a = ±√ (1 - sin^2 a )
Во второй четверти косинус отрицателен, значит:
cos a = - √ (1 - sin^2 a )
cos a = - √ (1 - 25/169)
cos a = - √ 144/169
cos a = - 12/13
Тогда тангенс (отношение синуса к косинусу) равен:
tg a = (5/13)/(-12/13) = - 5/12
ответ: cos a = - 12/13, tg a = - 5/12.
cos^2 a = 1 - sin^2 a
cos a = ±√ (1 - sin^2 a )
Во второй четверти косинус отрицателен, значит:
cos a = - √ (1 - sin^2 a )
cos a = - √ (1 - 25/169)
cos a = - √ 144/169
cos a = - 12/13
Тогда тангенс (отношение синуса к косинусу) равен:
tg a = (5/13)/(-12/13) = - 5/12
ответ: cos a = - 12/13, tg a = - 5/12.

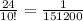

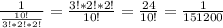
на фото...................