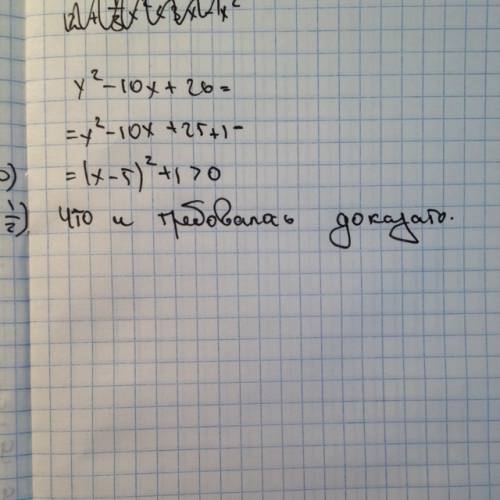
, где A, B, C - координаты нормального вектора плоскости N(A,B,C).
⇒ N(2,-3,4).
, где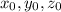 
- координаты точки M(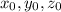), через которую проходит прямая, 
- координаты направляющего вектора S().) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).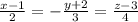
Пусть одна из сторон прямоугольника=a, a вторая=b.
Тогда
2a+2b=28(противоположные стороны прямоугольника равны)
и a+b=14(поделили выражение на 2)
a=14-b
диагональ прямоугольника делит его на 2 прямоугольных треугольника
Раасмотрим любой из треугольников
и
по теореме Пифагора :
a*a+b*b=10*10=100
a=14-b, тогда
(14-b)^2(в квадрате)+b^b=100
По формуле квадрата разности раскладываем выражение (14-b)^2
Получаем:
(14-b)^2=14^2-2*14*b+b^b=196-28b+b^2
a*a+b*b=196-28b+b^2+b^2=196-28b+2b^2
196-28b+2b^2=100
Переносим все в левую часть и получаем:
2b^2-28b+96=0
Поделим обе части уравнения на 2:
b^2-14b+48=0
d=B^2-4*A*C
d=196-4*48=4
b1=(14+2)/2=8
b2=(14-2)/2=6
При b=8
a=14-8=6
S=a*b=48см в квадрате
При b=6
a=14-6=8
S=a*b=48см в квадрате
ответ: 48см в квадрате
