Судя по содержанию учебника, комбинаторику и теорию вероятности в решении применять нежелательно?..)) Тогда так:
Для выполнения условия необходимо, чтобы:
1-й ученик получил тетради 2; 3 или 4
2-й ученик получил тетради 1; 3 или 4
3-й ученик получил тетради 1; 2 или 4
4-й ученик получил тетради 1; 2 или 3
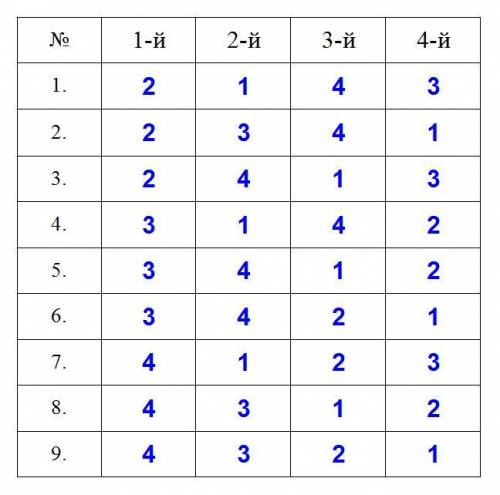
Все возможные варианты раздачи тетрадей ученикам так, чтобы ни один из них не получил свою тетрадь (числа обозначают номера тетрадей, в верхней строке - номера учеников): см. рис.
Как видно из таблицы, всего таких вариантов - 9.
Поскольку речь в задании идет не о величине вероятности, а о вариантах вероятности, то, скорее всего, ответ нужен именно такой.
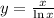
1. Область определения: На ноль делить нельзя -->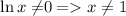 
и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
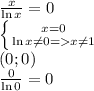Только одна точка (0;0)
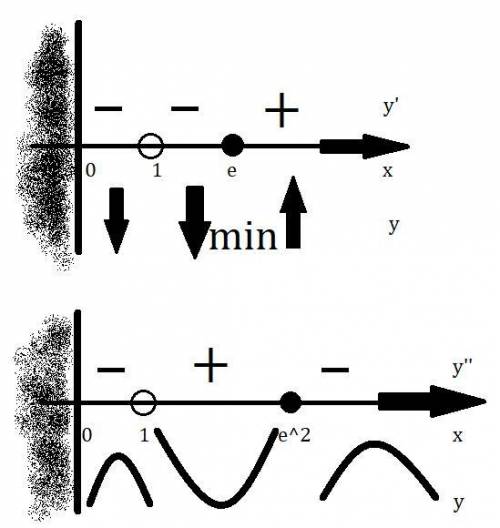
4. Исследование с 1ой производной:
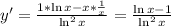
см. внизу.
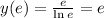
5. Исследование со 2ой производной:
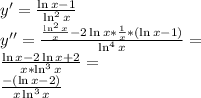
см. внизу.
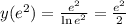
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: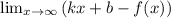 
Находим коэффициент k: 
Находим коэффициент b: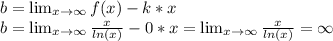 
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва: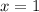 
Находим переделы в точке 1: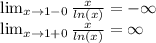 
Значит точка разрыва II рода и является вертикальной асимптотой.
(x+1)*(x+2)-x²=128
x²+2x+x+2-x²=128
3x=126
x=42
Наши числа 42 43 44