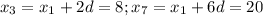
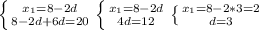
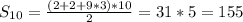

Объяснение: 4. (sin(β-π)×sin(2π-β)×cos(β-2π))/
/(sin(π/2 -β)×ctg(π-β)×ctg(β+ 3π/2)) =
=(sin(-(π-β))×sin(-β+2π)×cosβ)/(cosβ×(-ctgβ)×(-tgβ))=
=(-sinβ×(-sinβ)×cosβ)/(cosβ×ctgβ×tgβ)=(sin²β×cosβ)/(cosβ×1) =sin²β ;
5.
1+sinx×cosx×tgx = 1+ (sinx×cosx×sinx)/cosx= 1+ sin²x =1 + sin²(π/3)=
=1+(√3/2)² = 1+ 3/4 = (4+3)/4 = 7/4.
Здесь sin(π/3) = √3/2.
6. tgα=sinα/cosα , cosα=4/5,
Найдем sinα: sin²α= 1 - cos²α = 1 - (4/5)² = 1- (16/25) = (25-16)/25 =
= 9/25;
sinα = - √(9/25) = -3/5; sinα отрицательный потому что (3π/2)<α<2π ;
tgα= sinα/cosα = -(3/5)/(4/5) = -(3×5)/(5×4) = - 3/4.