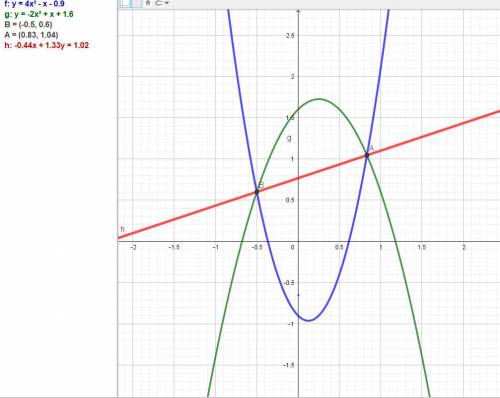
В точках пересечения значения функций совпадают, значит, можно определить координаты точек, приравняв уравнения.
4x² - x - (9/10) = -2x² + x + (8/5).
Получаем квадратное уравнение 6x² - 2x - (25/10) = 0.
Ищем дискриминант:
D=(-2)^2-4*6*(-2.5)=4-4*6*(-2.5)=4-24*(-2.5)=4-(-24*2.5)=4-(-60)=4+60=64;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√64-(-2))/(2*6)=(8-(-2))/(2*6)=(8+2)/(2*6)=10/(2*6)=10/12=5/6~~0.83333;
x_2=(-√64-(-2))/(2*6)=(-8-(-2))/(2*6)=(-8+2)/(2*6)=-6/(2*6)=-6/12=-0.5.
Находим значения "у".
y1 = -2*(25/36) + (5/6) + (8/5) = 94/15,
y2 = -2*(1/4) + (-1/2) + (8/5) = 3/5.
Имеем две точки А((5/6); (94/15)) и В(-1/2); (3/5)).
Вектор ВА = ((5/6)-(-1/2); ((94/15)-(3/5)) = (8/6); 85/15) = ((4/3); (17/3)).
Уравнение прямой через две точки пересечения:
(x - (5/6))/94/3) = (y - (94/15))/(17/3).
ответ: хЄ (- ∞ ; 1 ] .
Объяснение:
( x - 1 )| x² + 1 | + | x - 1 |( x² + 1 ) = 0 ;
( x - 1 )( x² + 1 ) + | x - 1 |( x² + 1 ) = 0 ;
( x² + 1 )( x - 1 + | x - 1 | ) = 0 ;
x² + 1 ≠ 0 або x - 1 + | x - 1 | = 0 ;
розв"язуємо останнє рівняння :
| x - 1 | = - х + 1 ;
вираз під модулем дорівнює 0 при х = 1 .
1) х ≤ 1 , тоді - ( x - 1 ) = - ( x - 1 ) ; правильна рівність при хЄ (- ∞ ; 1 ] ;
2) x > 1 , тоді x - 1 = - х + 1 ; > 2x = 2 ; > x = 1 ∉ ( 1 ; + ∞ ) .
В - дь : хЄ (- ∞ ; 1 ] .
или можно решить так.
b(n)=b1*q^(n-1)- формула n-ого члена
b(9)=b1*q^8
b(11)=b1*q^10
b(11)/b(9)= q^(10)/q^(8)= q^2
1/8 : (1/4)= 1/8 *4 = 1/2
q=V(1/2)= 1/V2= V2/2- знменатель прогрессии
b(1)= b(9)/ (q^8)
q^8= (V2/2)^8= 2^4/ 2^8= 1/2^4=1/16
b1= 1/4 : 1/16= 1/4* 16 = 4
надеюсь я вам