x = 8 или x = 28
p = 3
Объяснение:
По формуле разности квадратов x²-y²=(x-y)(x+y). Поскольку x и y — натуральные, то они целые, а значит, их сумма и разность тоже целые. Причем сумма натуральных чисел строго положительная, поэтому и разность для выполнения условия задачи должна быть положительной. Учитывая, что 55=5×11=1×55 и других разложений на натуральные множители нет, стало быть, один из множителей выражения x²-y² равен 5, а другой — 11, либо один равен 1, а другой — 55.

(8, 3)
или
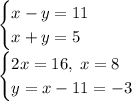
Вторая пара решений (8, -3) не удовлетворяет условию, потому что -3 — не натуральное.
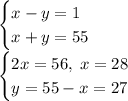
(28, 27)
или
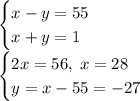
Четвертая пара (28, -27) не удовлетворяет условию, потому что -27 — не натуральное.
___________________________________
Немного преобразуем уравнение:
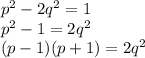
Как и в предыдущей задаче, p+1>0 и p-1>0 (p — простое, 2 — наименьшее простое число).
Правую часть можно представить в виде произведения двух натуральных множителей несколькими : 2q² = 1×2q² = 2×q² = 2q×q
Если один из множителей — 1, а другой — 2q², то только p-1 может быть равно 1 и p=2 (иначе p=0, 0 — не простое). Но тогда p+1=3=2q², q не будет целым.
Если один из множителей — 2, а другой — q², то только p-1 может быть равно 2 и p=3 (иначе p=1, 1 — не простое). Тогда p+1=4=q², q=2 — удовлетворяет условию
Пускай один из множителей — 2q, а другой — q. То есть один из них вдвое больше второго.
2(p-1)=p+1, 2p-2=p+1, p=3, в таком случае 2q²=2×4=8, q²=4, q=2 — удовлетворяет условию
или
p-1=2(p+1), p-1=2p+2, p = -3 — не простое
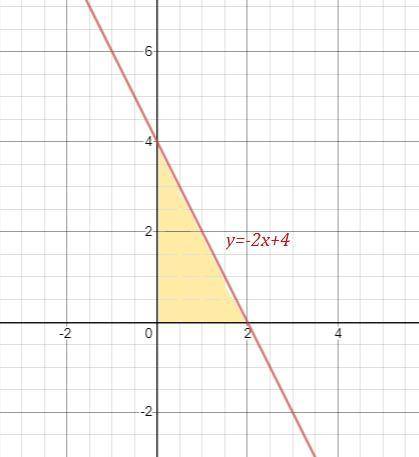
Уравнение прямой, отсекающей от первого координатного угла треугольник, имеет вид y=kx+b . Этот треугольник прямоугольный и его площадь равна половине произведения катетов.
Так как точка А(1;2) принадлежит этой прямой,то подставив координаты точки А(1;2) в это уравнение получим

Уравнение прямой теперь будет выглядеть так:  .
.
Найдём точки пересечения этой прямой с осями координат:
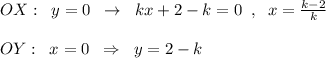
Длины отрезков, отсекаемых прямой y=kx+2-k на координатных осях, равны (2-k) на оси ОУ и (k-2)/k на оси ОХ. Эти отрезки и есть катеты прямоугольного треугольника. Вычислим его площадь:
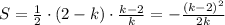
Найдём минимум это функции S(k).

Точка минимума:  , так как при переходе через k= -2 производная меняет знак с минуса на плюс.
, так как при переходе через k= -2 производная меняет знак с минуса на плюс.
При k= -2 уравнение искомой прямой будет
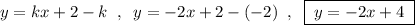
ответ: k= -2 .
2) х^2 - 11х + 24 = ( x - 8 )( x - 3 )
D = 121 - 96 = 25 = 5^2
X1 = ( 11 + 5 ) : 2 = 8
X2 = ( 11 - 5 ) : 2 = 3
3) ( ( x - 8 )( x + 8 )) / (( x - 8 )( x - 3 )) = ( x + 8 ) / ( x - 3 )
ответ ( Х + 8 ) / ( Х - 3 )