Посчитаем сначала количество чисел, записываемых цифрами от 
до 
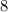, а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до :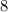 
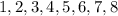. Любые 
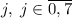вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: 
.
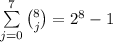Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из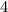 
-ех оставшихся чисел. Поскольку четверок подряд идущих 
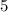, то всего искомых чисел 
.
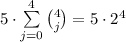Итого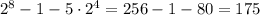 
.
1. Нет. Одночлен - это произведение числовых и буквенных множителей и их степеней.
2. Да
3. Да. Или если точнее, то буквенный множитель (коэффициент) - число, стоящее перед буквой.
4. Да
5. Нет. Коэффициент одночлена - числовой множитель одночлена, записанный в стандартном виде.
6. Да
7. Нет. Подобные одночлены - одночлены, имеющие общий коэффициент.
8. Да
9. Да
10. Да. Если точнее, то одночлены, записанные в стандартном виде, называется многочленом стандартного вида.
11. Нет. Чтобы привести подобные члены, нужно сложить числовые множители и умножить на буквенное выражение.
12. Да
13. Да.
а) (an): 1, 2, 4, ...
Так как 4:2=2:1=2=q, то (an) геометрическая прогрессия со знаменателем q=2. Тогда продолжение имеет вид:
(4·2=) 8, (8·2=) 16, (16·2=) 32, ...
(bn): -15, -12, -9, ...
Так как -12-(-15)=-9-(-12)=3=d, то (bn) арифметическая прогрессия с разностью d=3. Тогда продолжение имеет вид:
(-9+3=) -6, (-6+3=) -3, (-3+3=) 0, ...
b) Двадцатый член арифметической прогрессии равен:
b20=b1+19·d= -15+19·3 = -15+57 = 42.