Если ещё не изучено понятие производной, то решение может быть таким:
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
Объяснение:
х км/ч - скорость катера в стоячей воде;
(x-2) км/ч - скорость катера против течения;
(x+2) км/ч - скорость катера по течению;
20/(x+2) ч - время, пройденное по течению;
8/(x-2) ч - время, пройденное против течения.
На весь путь катер затратил 2 часа, составим уравнение
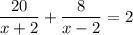
Домножив обе части уравнения на 0.5(x+2)(x-2), получаем
10(x-2) + 4(x+2) = (x+2)(x-2)
10x - 20 + 4x + 8 = x² - 4
x² - 14x + 8 = 0
D = 14² - 4 * 1 * 8 = 164
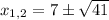
Корень 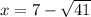 не удовлетворяет условию.
не удовлетворяет условию.
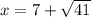 - скорость катера в стоячей воде, что странный корень вышел(
- скорость катера в стоячей воде, что странный корень вышел(
8*sin(x) + 7*cos(6*I*p + x) = 2*\/ 2 *\/ sin(x) + 7*cos(6*I*p + x) + 57 / / \\ / / \\
| |115 \/ 229 || | |115 \/ 229 ||
x1 = I*im|asin|--- +|| + re|asin|--- +| |
\ \ 16 16 // \ \ 16 16 // дано уравнение
8 \sin{\left (x \right )} + 7 \cos{\left (6 i p + x \right )} = 2 \sqrt{2} \sqrt{\sin{\left (x \right )}} + 7 \cos{\left (6 i p + x \right )} + 57$$
преобразуем
- 2 \sqrt{2} \sqrt{\sin{\left (x \right )}} - 7 \cos{\left (6 i p + x \right )} - 57 + 8 \sin{\left (x \right )} + 7 \cos{\left (6 i p + x \right )} = 0
сделаем замену
w = \sin{\left (6 i p + x \right )}
- 2 \sqrt{2} \sqrt{w} = - 8 w + 57
возведём обе части уравнения в (0) 2-ую степень
8 w = \left(- 8 w + 57 \right)^{2}
8 w = 64 w^{2} - 912 w + 3249
перенесём правую часть уравнения в левую со знаком минус
- 64 w^{2} + 920 w + 3249 = 0
это уравнение вида
a*w^2 + b*w + c = 0
квадратное уравнение можно решить с дискриминанта.
корни квадратного уравнения:
w_{1} = \frac{\sqrt{D} - b}{2 a}
w_{2} = \frac{- \sqrt{D} - b}{2 a}
где D = b^2 - 4*a*c - это дискриминант
т.к.
a = - 64
b = 920
c = - 3249
,то
D = b^2 - 4*a*c = (920)^2 - 4 * (-64) * (-3249) = 14656
т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
w_{1} = - \frac{\sqrt{229}}{16} + \frac{115}{16}
w_{2} = \frac{\sqrt{229}}{16} + \frac{115}{16}
т.к.
\sqrt{w} = 2 \sqrt{2} w - \frac{57 \sqrt{2}}{4}
и
\sqrt{w} \geq 0
то
___
57*\/ 2 ___
- + 2*w*\/ 2 >= 0
4
или
$$\frac{57}{8} \led w$$
$$w < \infty$$
тогда, окончательный ответ:
$$w_{2} = \frac{\sqrt{229}}{16} + \frac{115}{16}$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
дано уравнение
$$\sin{\left (x \right )} = w$$
это простейшее тригонометрическое уравнение
это уравнение преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n - \operatorname{asin}{\left (w \right )} + \pi$$
или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n - \operatorname{asin}{\left (w \right )} + \pi$$
, где n-любое целое число
подставляем w:
x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
x_{1} = 2 \pi n + \operatorname{asin}{\left (\frac{\sqrt{229}}{16} + \frac{\sqrt{115}{16} \right )}
x_{1} = 2 \pi n + \operatorname{asin}{\left (\frac{\sqrt{229}}{16} + \frac{\sqrt{115}{16} \right )}
x_{2} = 2 \pi n - \operatorname{asin}{\left (w_{1} \right )} + \pi
x_{2} = 2 \pi n + \pi - \operatorname{asin}{\left (\frac{\sqrt{229}}{16} + \frac{\sqrt{115}{16} \right )}
x_{2} = 2 \pi n + \pi - \operatorname{asin}{\left (\frac{\sqrt{229}}{16} + \frac{\sqrt{115}{16} \right )}