Известно что 2(3x+a)^2=18x^2+60x+2a^2 найдите a и вычислите значение выражения 2(3x+a)^2 при х= -3

Question

Алгебра: Известно что 2(3x+a)^2=18x^2+60x+2a^2 найдите a и вычислите значение выражения 2(3x+a)^2 при х= -3

арсюха6 · Accepted Answer

К числителю и знаменателю нужно прибавить число 1.

Объяснение:

Имеется дробь 3/7. К числителю и знаменателю этой дроби нужно прибавить одно и то же число, чтобы получить дробь 1/2. Т.е. нужно прибавить такое число, чтобы числитель был в 2 раза меньше знаменателя.

Допустим, нужно прибавить некоторое число x. Тогда числитель (3+x) будет в 2 раза меньше знаменателя (7 + x). Запишем в виде уравнения:

2(3 + x) = 7 + x;

6 + 2x = 7 + x;

2x - x = 7 - 6;

x = 1. ⇒ К числителю и знаменателю нужно прибавить число 1.

Проверка:

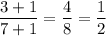$\displaystyle \frac{3+1}{7+1} = \frac{4}{8} = \frac{1}{2}$ .

MOGZ ответил