На фотографии.
Объяснение:
Тут ситуация весьма неоднозначна. Тут будет аж две фигуры ограниченных этими графиками и осью Ox. Я нашёл и первую и вторую, какую вам выбрать и предоставить преподавателю, решать вам ;) ответ в обоих случаях получился примерным, потому что графики пересекаются не в целой точке. Решение для нахождения первой фигуры я обозначил римской цифрой 1, а второй - 2.
P.S. Я не понимаю, зачем преподаватели задают такие задания.
Вот, надеюсь, правильно. Желаю удачи.
P.P.S Сейчас я понял, что этих фигур ещё оказывается 3
0_0 Но, я думаю 2 будет достаточно :) Задание - найти ФИГУРУ. По идее, одну.

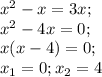
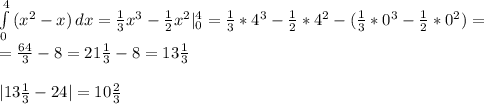
(a+b)(a-b)=a^2-b^2