Пусть Х деталей токарь должен был обрабатывать за 1 час. Тогда время его работы составило бы (240:Х) часов. Но токарь стал обрабатывать в час на 2 детали больше, то есть (Х+2), и время его работы составило 240:(Х+2) часов. Зная, что токарь выполнил задание на 4 часа раньше срока, составим уравнение:
240:Х-240:(Х+2)=4
240*(Х+2)-240*Х=4*Х*(Х+2)
4*Х^2+8*Х-240*Х-480+240*Х=0
4*Х^2+8*Х-480=0
Х^2+2*Х-120=0
Дискриминант=484
Корень из дискриминанта=22
Х1=-11
Х2=10.
так как количество деталей величина положительная, то -11 - посторонний корень. Значит, токарь должен был обрабатывать за 1 час 10 деталей.
Такого значения параметра
b не существует.
Объяснение:
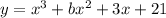
Находим производную
у'=

Приравниваем производную 0:
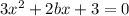
функция только убывает, если
на всей области определения
у'<0.
==>
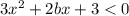
Рассмотрим уравнение:
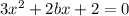
Это уравнение квадратичной
функции. Старший коэффици
ент а=3>0 ==>
если представить ее график
- это парабола, ветви которой
напрвлены вверх (парабола не
может полностью находиться
под осью абсцисс, так
как ее ветви бесконечно про
должаются вверх).
Вывод:
Условие у'<0 невыполнимо.
==> не существует такого зна
чения параметра b, когда функ
ция
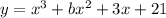
убывает на всей области оп
ределения.
пусть х²=а, а≥0
а²-7а+6=0
D=49-24=25
a=(7-5):2=1
a=(7+5):2=6
x²=1 x²=6
x=1; x=-1 x=√6; x=-√6
ответ: -1;1;-√6;√6