Произведение чисел, переменных и их степеней называется одночленом, например,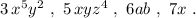 
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
,
.
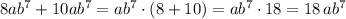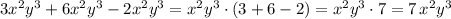Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
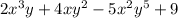не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов, но в результате всё равно получим многочлен:
.
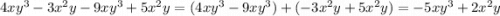Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
,
.
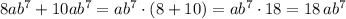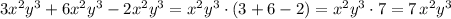Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
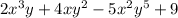не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов.
.
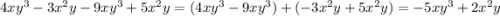Представим множество возможных исходов как квадрат 60x60 на плоскости Oxy (0 <= x <= 60, 0 <= y <= 60), x - время, в которое на встречу пришел один человек, y - другой. "Отметим" на нем множество благоприятных исходов, когда встреча состоялась: ему соответствует область, для которой выполняется условие |x - y| <= 18 (они пришли на место встречи с разницей во времени <= 18 минут).
Границы области - прямые y = x + 18 и y = x - 18. Отношение площади фигуры, ограниченной этими прямыми, ко всей площади квадрата - и есть вероятность удачной встречи.
Площадь фигуры удобно искать, вычитая из площади квадрата площади треугольников в левом-верхнем и правом-нижнем углах.
60^2 - 1/2 (60-18)^2 - 1/2 (60-18)^2 = 3600 - 1764 = 1836
Искомая вероятность = 1836 / 3600 = 0,51