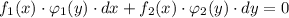
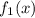 и
и 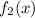 зависят только от переменной "х" , а функции
зависят только от переменной "х" , а функции 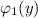 и
и 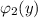 зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" .
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 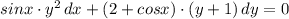 .
. 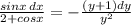 .
.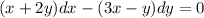 , то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения
, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 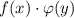 .
.
логарифмическое квадратное неравенство, замена переменной:
t²-7t+12≥0 метод интервалов:
1.t²-7t+12=0, t₁=3, t₂=4
2. ++++[3]-----[4]+++++>t
3. t≤3, t≥4
обратная замена:
1. t≤3. log₂(25-x²)≤3 , 3=log₂2³=log₂8
log₂(25-x²) ≤ log₂8
ОДЗ: 25-x²>0. (5-x)*(5+x)>0
-5<x<5
основание логарифма а=2, 2>1 знак неравенства не меняем
25-x²≤8, 17-x²≤0. (√17-x)*(√17+x)≤0
x≤-√17, x≥√17
учитывая ОДЗ, получим:
x∈(-5;-√17]∪[√17;5)
2. t≥4, log₂(25-x²)≥4. 4=log₂2⁴=log₂16
log₂(25-x²)≥log₂16, 25-x²≥16. 9-x²≥0. (3-x)*(3+x)≥0
-3≤x≤3. учитывая ОДЗ, получим: x∈[-3;3]
ответ: x∈(-5;-√17)∪[√17;5)∪[-3;3]