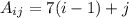(при движении в строке (меняя номер столбца) увеличиваем значение на 1, и изначально значение должно быть равно 1; при движении в столбце (изменяя номер строки) увеличиваем на 7, при этом изначально эта часть должна равняться 0)![S = [7(i_{1}-1)+j_{1}] + [7(i_{2}-1)+j_{2}] + [7(i_{3}-1)+j_{3}] + [7(i_{4}-1)+j_{4}] + [7(i_{5}-1)+j_{5}] + [7(i_{6}-1)+j_{6}] + [7(i_{7}-1)+j_{7}] = 7(i_{1}+i_{2}+i_{3}+i_{4}+i_{5}+i_{6}+i_{7}-7) + j_{1}+j_{2}+j_{3}+j_{4}+j_{5}+j_{6}+j_{7}](/tpl/images/0813/6728/e7629.png)
5)
cos(60 + α)=cos60cosα-sin60sinα
Во первых, Синус 60=√3\2, а Косинус 1/2. Во вторых синус альфа=√2\2 может быть только у угла 45 градусов. У этого угла синус и косинус равны. Теперь можем это всё подставить:
1/2*√2\2-√3\2*√2\2=√2\4-√6\4=(√2-√6)/4