m = p1^d1 * p2^d2 * p3^d3 * ... * pk^dk
n = p1^q1 * p2^q2 * p3^q3 * ... * pk^qk
Степени могут быть нулеывми.
Где p - простое. Рядом стоящая цифра - индекс.
^ - степень.
m + n = min(p1^d1, p1^q1) * min(p2^d2, p2^q2) * ... * min(pk^dk,pk^qk) + max(p1^d1,p1^q1)* ... * max(pk^dk, pk^qk)
С другой сторноы
m+n = p1^d1*p2^d2+p3^d3*...*pk^dk+p1^q1*p2^q2*...*pk^qk
Чтоб торжество было верно d1 > q1, d2 > q2, d3>q3, ... , dk > qk;
или наоборот d1 < q1, d2 < q2, d3 < q3, ... , dk < qk. Конец решения.
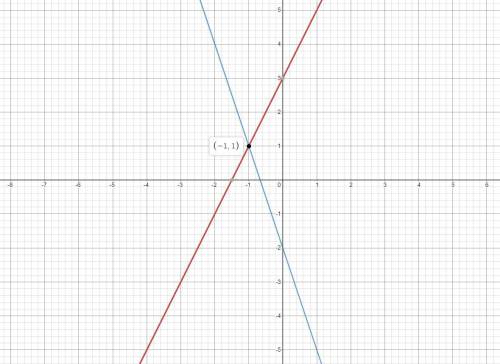
(-1; 1)
Объяснение:
Сложение (как эту систему решать надо):
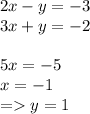
Подстановка (самый универсальный
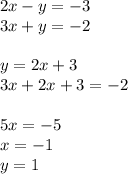
Графический (самый неудобный долгий, далеко не всегда ты можешь построить график по уравнению (т.е. надо еще поведение функции изучить + есть риск погрешности (а она, если корни нецелые будет всегда), поэтому каждое решение надо проверять; надо научиться решать этим методом, чтобы потом больше никогда им не пользоваться; в данном случае у тебя 2 пересекающиеся прямые; строим их и находим координаты точки пересечения).
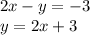
Таблица:
x=0; y=3
x=1; y=5
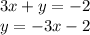
Таблица:
x=0; y=-2
x=1; y=-5
Построение (см. фото)
Проверка выполнена устно (просто в каждое уравнение подставить и проверить равенство на истинность)
Две другие системы решаются аналогично.
23*7,5=17,25*(х+1)
172.5 =17,25х+17,25
172,5-17,25=17.25х
155.25=17.25х
х=9