1) Допустим, было 
граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было 
.
Составляем уравнение:
5% · + 10% ·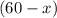 
= 8% · 60;
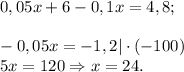
Тогда 5%-ого раствора было 24 г, а 10% - 60 - 24 = 36 (г).
ОТВЕТ: 5%-ого - 24 г, 10%-ого - 36 г.
2) Допусти, у нас есть "десятирублевок". Тогда "пятирублевок" всего 
.
Составляем уравнение:
Десятирублевых монет - 7. Пятирублевых - 25 - 7 = 18
ОТВЕТ: десятирублевых - 7; пятирублевых - 18.
3) Пусть вагон весит т. Тогда электровоз стоит 
.
Составляем уравнение:
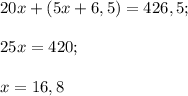
Один вагон весит 16,8 т. Тогда электровоз весит 5 · 16,8 + 6,5 = 90,5 (т).
ОТВЕТ: вагон весит 16,8 т, электровоз - 90,5 т.
— один из частных случаев степенной функции. Эта функция не имеет своего собственного имени (в отличие от квадратичной функции или кубической функции) и называется просто формулой. График функции y равен корню из x — ветвь параболы.
Для построения графика возьмём несколько точек. Так как под знаком квадратного корня могут стоять только неотрицательные числа, значения аргумента должны бить неотрицательными. Для удобства вычислений берём x, квадратные корни из которых — целые числа:
\[x = 0;y = \sqrt 0 = 0;\]
\[x = 1;y = \sqrt 1 = 1;\]
\[x = 4;y = \sqrt 4 = 2;\]
\[x = 9;y = \sqrt 9 = 3;\]
\[x = 16;y = \sqrt {16} = 4;\]
и т.д. Таким образом, получили точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
Результаты удобнее оформить в виде таблицы:
7<sqrt(61)<8
между 7 и 8