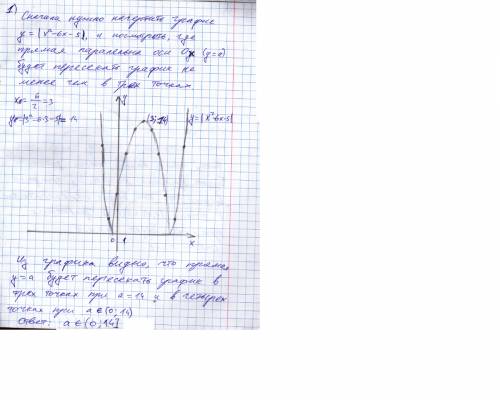
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



Дано функцію f(x) = (x^2-8x)/(x+1)
Знаходимо найбільше і найменше значення даної функції на проміжку [-5,-2].
f(-5) = ((-5)^2-8*(-5))/(-5+1) = 65/(-4) = -16,25.
f(-2) = ((-2)^2-8*(-2))/(-2+1) = 20/(-1) = -20.
Визначаємо точки екстремуму даної функції.
Знаходимо первісну:
f'(x) = (2x-8)*(x+1) - 1*(x^2-8x))/((x+1)^2) = (x^2 + 2x - 8)/((x + 1)^2).
Прирівнюємо їі до 0 (достатьно чисельник):
x^2 + 2x - 8 = 0, Д = 4+4*8 = 36, х1 = (-2 - 6)/2 = -4, х2 = (-2 + 6)/2 = 2.
Знаходимо знаки первісної:
х = -5 -4 1 2 3
y' = 0,4375 0 -1,25 0 0,4375 .
У точці х = -4 маємо максимум функції,
f(-4) = ((-4)^2-8*(-4))/(-4+1) = 48/(-3) = -16.
Відповідь:
- найбільше значення даної функції на проміжку [-5,-2] дорівнює -16,
- найменше значення даної функції на проміжку [-5,-2] дорівнює -20,
- максимум функції у точці х = -4,
- мінімум функції у точці х = 2.
значит наша функция, проходящая через данную точку задана уравнением
5=(-6/3)+b b=5+2=7 отсюда график искомой функции
y=(-1/3)*x+7