Определим общее число расстановок на пяти позициях 5 шариков:
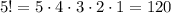
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах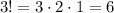 
Таким образом, всего имеется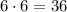 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
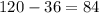
ответ: 84
Теорема Виета позволяет быстрее решать приведенные квадратные уравнения, не прибегая к объемному решения через дискриминант.
Приведенными квадратными уравнениями называются те квадратные уравнения, в которых коэффициент а=1 (для формулы ax²+bx+c=0)
То есть, общий вид этих уравнений таков: x²+bx+c=0
Согласно теореме, сумма решений уравнения равна противоположному значению коэффициента b, а произведение решений равно коэффициенту с:
x₁+x₂=-b
x₁*x₂=c
Решаются такие уравнения подбором чисел, которые подходили бы под оба условия теоремы. Например:
x²+6x+8=0
x₁+x₂=-6
x₁*x₂=8
Мы видим, что сумма решений отрицательна, значит как минимум одно из решений меньше нуля. В таком случае, произведение тоже было бы отрицательным, но это не так. Значит оба решения меньше нуля. Вспоминаем, какие числа при умножении дают 8:
-1 и -8 не подходит, так как -1+(-8)=-9, а не -6, как нужно нам
-2 и -4 подходит, так как -2+(-4)=-6, а -2*(-4)=8
Следовательно, решениями являются числа -2 и -6, так как соответствуют обоим условиям теоремы.
4 общих точки - это и есть решение.
построить график просто - строится функция под модулем и потом все отрицательные значения отражают симметрично оси х вверх.