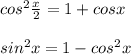
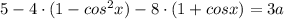
Получаем квадратное уравнение относительно
cosx=t
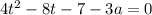
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
За 6 часов первый пройдёт 3·6=18 км, а второй пройдёт 4·6=24 км.
Но! Двигаются они не вдоль одной прямой. Их траектории - это катеты прямоугольного треугольника (двигались-то они не на север и юг, а на север и запад). А расстояние между ними - это гипотенуза прямоугольного треугольника.
Гипотенузу можно найти по теореме Пифагора: сумма квадратов катетов равна квадрату гипотенузы. То есть:
a²+b²=c², где a и b - катеты, т.е. пути наших туристов.
Подставим числа:
18²+24² = 900
Обратим внимание: 900 - это не гипотенуза. 900 - это квадрат гипотенузы. Поэтому, чтобы найти гипотенузу, извлечём квадратный корень из 900:
√900 = 30
Я это только записал как корень, хотя число, дающее в квадрате 900, подбирается элементарно.
Как бы то ни было, 30 - это гипотенуза, это наш ответ. Запишем его.
ответ: через 6 часов расстояние между ними будет равняться 30 км.