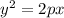ее фокус находится в точке с координатами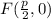 
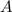находиться в системе уравнения 
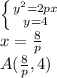Если уравнение касательной равна 
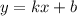с учетом того что она проходит через точку 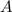получаем 
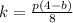, подставляя 
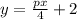
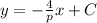он проходит через точку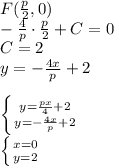 
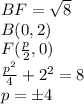
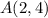
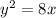
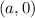центр окружности (так как центр лежит на оси 
) 
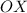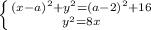
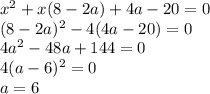
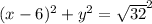
т.к основания у логарифмов разные то можно воспользовать формулой т.е logx(3)=1/log3(x)
Получатся логарифмы одинаковые .
Для удобства заменим log3(x)=t
Получим квадратное уравнение: t^2-2t+1=0. D=0. x1,2=1
так как log3(x)=t то log3(x)=1 и x=3
Вот и все)