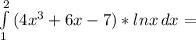
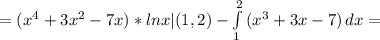
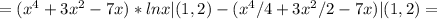
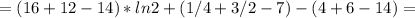
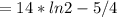
– есть целый корень кратности 
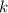многочлена 
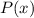, то многочлен будет делиться нацело на 
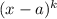и не будет делиться нацело на 
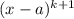(это следует из теоремы Безу). является целым корнем многочлена, то свободный его член (равный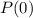 
) должен делиться на 
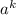. Число 
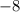делится нацело на 
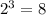(на число 
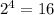нацело не делится): значит кратность корня 
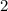не может превышать 
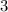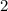. вообще является корнем этого многочле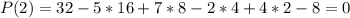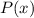на:
на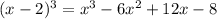 
– если поделится, то корень 2 имеет кратность :
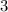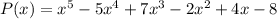
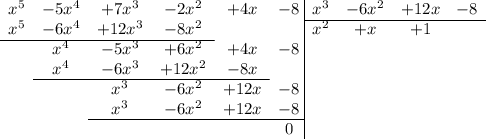
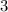(из-за того, что свободный член не делится на 
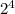нам не надо проверять делимость многочлена на 
).
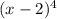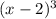не вышло, нам пришлось бы делить многочлен на 
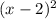и т.д. 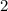корень 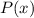кратности .
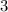