Здесь есть несколько простых правил. Смотри:
1) 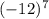 и
и 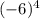
Есть правило о том, что любое число в чётной степени всегда 
То есть если мы (-6) возводим в чётную степень 4, то знак меняется с "минуса" на "плюс".
А вот с нечётной степенью это не работает. То есть если мы возводим (-12) в нечётную степень 7, то знак остаётся такой, какой был. А мы знаем, что любое отрицательное число всегда меньше положительного. Поэтому 
2) 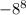 и
и 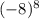
Здесь ещё проще. Под числом -8 мы понимаем -1*8. В первом случае (где без скобок записано) в восьмую степень возводится только сама 8, а "минус единица", можно сказать, остаётся за скобкой. Примитивно можем записать так:

Поэтому когда возводим 8 в восьмую (чётную) степень, знак всё равно не меняется, так как - 1 у нас осталось с таким же знаком "минус".
А вот во втором случае (где скобки) скобками нам показывают, что в чётную степень 8 возводиться как - 1, так и сама 8. Поэтому как ни крути, получим положительное число:

Значит, 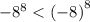
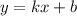 - уравнение прямой на координатной плоскости,
- уравнение прямой на координатной плоскости,
где  - угловой коэффициент.
- угловой коэффициент.
1) Известен угловой коэффициент первой прямой 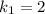 .
.
2) Противоположная сторона квадрата лежит на прямой, параллельной первой прямой, а необходимым и достаточным условием их параллельности является равенство их угловых коэффициентов.
Получаем:
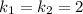
3) Две остальные стороны квадрата лежат на прямых, перпендикулярных первой прямой, а для этого необходимо и достаточно, чтобы их угловые были обратны по величине и противоположны по знаку.
Получаем:

4) а теперь найдём сумму угловых коэффициентов трех прямых.
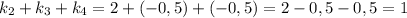

ответ: 1
б) (4 - 3√5)² = 16-24√5+45 = 61-24√5
в) 2 х 4х
+ - = 0 | (x²-9)
х+3 х-3 х²-9
2(x-3) + x(x+3) - 4x 2x-6+x²+3x-4x x²+2x+3x-4x-6
= = =
x²-9 x²-9 x²-9
x²-x-6 (здесь дискриминантом решается) (x-3)(x+2)
= = (x-3) сокращ.
x²-9 (x-3)(x+3)
x+2
и остается =
x+3
5x²-16x+3 (по D) 5(x-3)(x-0.2) (x-3)(5x-1) x-3
г) = = =
25x²-1 (5x+1)(5x-1) (5x+1)(5x-1) 5x+1
д) 3x+3-4+2x-11>0
5x-12>0
5x>12
x>2.4
как-то так, извиняюсьь