![[ -\frac{\pi}{2} ; \frac{\pi}{2} ]](/tpl/images/0597/4634/fea20.png) возрастает, а на промежутке
возрастает, а на промежутке ![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) - убывает
- убывает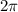 , то:
, то:![[ -\frac{\pi}{2}+2\pi n ; \frac{\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/22506.png) - промежутки возрастания синусоиды
- промежутки возрастания синусоиды![[ \frac{\pi}{2}+2\pi n ; \frac{3\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/745d6.png) - промежутки убывания синусоиды
- промежутки убывания синусоиды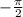 и точка
и точка 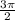 - одна и та же точка на тригонометрическом круге
- одна и та же точка на тригонометрическом круге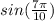 и
и 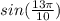
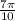
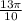
![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) убывания. Так как это промежуток убывания, то если выполняется
убывания. Так как это промежуток убывания, то если выполняется 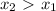 , то будет выполнятся
, то будет выполнятся 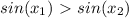
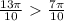
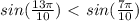
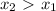 , то выполняется
, то выполняется 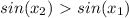
![[ \frac{3\pi}{2} ; \frac{5\pi}{2}]](/tpl/images/0597/4634/0c4f5.png)
![[- \frac{3\pi}{2} ; -\frac{\pi}{2} ]](/tpl/images/0597/4634/7af0d.png)
![[ \frac{3\pi}{2} ; \frac{5\pi}{2} ]](/tpl/images/0597/4634/5d6a9.png)
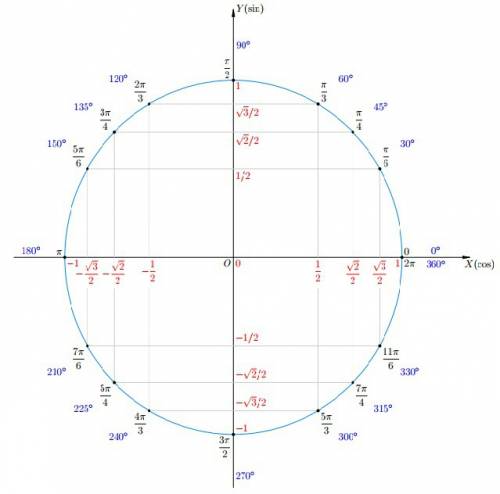
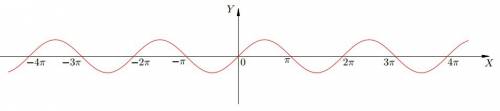
очевидно: (2cos4x -cos2x)² ≤ 9 и 9 + cos²5x ≥ 9 .
Если уравнение имеет решение,то одновременно должны выполнятся
(2cos4x -cos2x)² = 9 и 9 + cos²5x = 9 ⇔
{ (2cos4x -cos2x)² = 9 ; cos5x =0.
Нужно найти решения этой системы.
(2cos4x -cos2x)² = 9 ⇔ 2cos4x -cos2x = ± 3⇔ 2(2cos²2x -1) - cos2x = ± 3⇔ 2(2cos²2x - 1) - cos2x = ± 3 ⇔ 4cos²2x - cos2x - 2 = ± 3 .
a)
4cos²2x - cos2x -2 = - 3 ;
4cos²2x - cos2x+1 =0 квадратное уравнение относительно cos2x =t
D =1² -4*4*1 = -15 < 0 ⇒ не имеет решения
b)
2cos4x - cos2x = 3 ; * * * cos4x =1 и cos2x = -1⇔2cos²2x -1 =1и cos2x = -1* *
4cos²2x - cos2x -2 = 3 ;
4cos²2x - cos2x - 5 =0 ; D =1² + 4*4*(-5) =81 =9²
cos2x =(1 +9)/8 =5/4 >0 ⇒ x ∈ ∅ ;
cos2x =(1 -9)/8 = - 1 ⇒ 2x = π +2πm , m∈Z ⇔ x = π /2 +πm , m∈Z.
одновременно с этим (необходимо и достаточно)
cos5x =0⇒ 5x =π/2 +π*n , n ∈Z ⇔x = π/10+(π/5)*n.
---
{ x = π /2 +πm , x = π/10+(π/5)*n , m , n ∈ Z.
---
π /2 +πm = π/10+(π/5)*n ;
10 +20m = 2 +4n ;
n =4 +5m .
* * * серия решений x = π/10+(π/5)*n содержит решения x=π /2 +πm.* * *
ответ : x = π/10+(π/5)*n , n∈Z.