Биквадратное уравнение.
Решается заменой переменной:

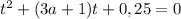
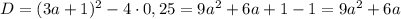
Если D >0, т.е.


уравнение имеет корни:
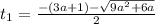 или
или 
Обратный переход:
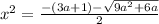 или
или 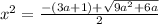
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
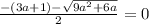
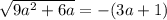
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
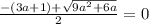
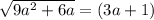
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 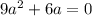
 или
или 
При 
уравнение принимает вид:

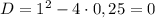 ⇒
⇒ 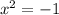
уравнение не имеет корней
При 
уравнение принимает вид:

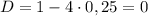 ⇒
⇒ 
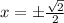
Уравнение 4-ой степени, значит
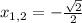 и
и 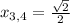
О т в е т. При 
(см. объяснение)
Объяснение:
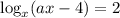
ОДЗ:
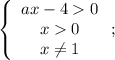
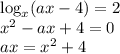
Заметим, что для любого корня уравнения вне зависимости от значения параметра  произведение
произведение 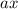 будет больше или равно 4.
будет больше или равно 4.
Причем 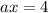 , если
, если 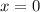 - корень уравнения. Но это невозможно, так как при
- корень уравнения. Но это невозможно, так как при 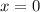 имеем
имеем 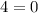 (неверно) при любом значении параметра.
(неверно) при любом значении параметра.
Тогда 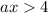 , то есть условие ОДЗ
, то есть условие ОДЗ  будет выполнятся всегда.
будет выполнятся всегда.
Исходное уравнение будет иметь ровно один корень, либо если 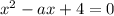 имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
Рассмотрим первый случай. Он достижим, когда 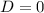 .
.
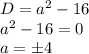
При 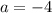 уравнение имеет корень
уравнение имеет корень  , поэтому такое значение параметра не подходит.
, поэтому такое значение параметра не подходит.
При 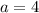 уравнение имеет корень
уравнение имеет корень 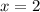 , поэтому такое значение параметра подходит.
, поэтому такое значение параметра подходит.
Рассмотрим второй случай. Он достижим, когда 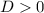 .
.
Здесь также важно, чтобы уравнение либо имело один корень  , а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
, а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
Обратимся к первой ситуации:
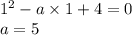
В этом случае уравнение имеет корни  или
или 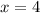 , первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
, первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
Для того чтобы вторая ситуация могла быть достижимой, необходимо, но не достаточно, чтобы выполнялось условие 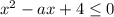 при
при 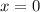 . Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
. Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
Итого при 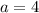 или
или  исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!