Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру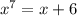 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
найдём точку пересечения прямых
4y=3x ⇒ 12y=9x ⇒ 5x+12y=5x+9x=14x ⇒ 14x=10 ⇒ x = 5/7 ⇒ 4y=3·5/7=15/7 ⇒ y=15/28
найдём векторы нормали
-3x+4y=0 ⇒ n₁(-3;4)
5x+12y-10=0 ⇒ n₂(5;12)
Проверим, острый ли угол между n₁ и n₂ (равносильно n₁·n₂ > 0)
n₁·n₂=-3·5+4·12=-15+48 > 0
Находим единичные вектора нормали
n₁'=n₁/|n₁|=(-3;4)/√(3²+4²)=(-3/5;4/5)
n₂'=n₂/|n₂|=(5;12)/√(5²+12²)=(5/13;12/13)
Находим вектор нормали к биссектрисе острого угла между прямыми
n₃=n₁'+n₂'=(-14/65;112/65)
Другим вектором нормали будет n₃'=65/14 n₃=(-1;8)
Составляем уравнение биссектрисы по точке (5/7;15/28) и вектору нормали n₃
n₃'·(x,y)=n₃'·(5/7;15/28) ⇒ -x + 8y = -5/7 + 8 ·15/28 = 25 / 7, или
-7x + 56y = 25
другой возможный вариант решения, использовать тот факт, что любая точка биссектрисы равноудалена от двух данных прямых, и формулу расстояния от точки до прямой
|4y-3x|/√(4²+3²) = |5x+12y-10|/√(5²+12²)
13|4y-3x| = 5|5x+12y-10|
13(4y-3x) = ±5(5x+12y-10)
Один вариант знака даёт биссектрису острого угла, второй — биссектрису тупого угла, потом останется только разобраться, какой вариант к какой биссектрисе относится.
