Привет! В первом если раскрыть скобки а^2 + ав -ав+в^2 = а^2+в^2
так как ав и -ав взаимо уничтожаются . Получается а^2+в^2
Во втором случае также а^2+ ав -ав - в^2= а^2-в^2
В примере 3 можно раскрыть скобки а^2 + ав + ав + в^2= а^2+2ав+в^2
Все примеры тождественно равны.
Есть еще формула квадрата суммы двух выражений
^2 - в квадрате
Объяснение:
Привет! В первом если раскрыть скобки а^2 + ав -ав+в^2 = а^2+в^2
так как ав и -ав взаимо уничтожаются . Получается а^2+в^2
Во втором случае также а^2+ ав -ав - в^2= а^2-в^2
В примере 3 можно раскрыть скобки а^2 + ав + ав + в^2= а^2+2ав+в^2
Все примеры тождественно равны.
Есть еще формула квадрата суммы двух выражений
^2 - в квадрате
a ∈ ∅
Объяснение:
Графиком трехчлена в левой части является парабола. В таком случае, условие "меньше 0" означает, что график лежит целиком под осью абсцисс, а ветви параболы направлены вниз ( a<0 ).
Если график лежит целиком под осью абсцисс, то нет пересечения графика с осью x, что равносильно отсутствию действительных корней квадратного трехчлена (дискриминант меньше 0).
Т.к. ветви параболы направлены вниз, то параметр a можно представить в виде:
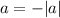
Тогда дискриминант равен:
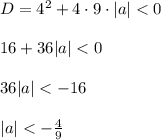
Получили противоречие (модуль не может быть отрицательным).
Значит не существует такого параметра a, при котором неравенство будет верно при любых значениях x