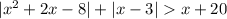
Имеем неравенство, содержащее несколько модулей.
Если неравенство содержит несколько различных модулей, то находят значения  , при которых выражение, стоящее под знаком модуля, равно нулю. Найденные значения
, при которых выражение, стоящее под знаком модуля, равно нулю. Найденные значения  разбивают числовую прямую на интервалы, на каждом из которых выражение под модулем сохраняет знак. А потом на каждом интервале раскрывают модули и решают полученную систему. Объединение решений составляет множество решений данного неравенства.
разбивают числовую прямую на интервалы, на каждом из которых выражение под модулем сохраняет знак. А потом на каждом интервале раскрывают модули и решают полученную систему. Объединение решений составляет множество решений данного неравенства.
1) Найдем нули модулей:
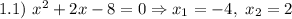
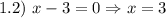
2) Начертим числовую координатную прямую и отметим найденные нули модулей, которые разбивают данную ось на 4 области (см. вложение).
3) Решим систему уравнений на каждом интервале, раскрывая модуль на каждом участке с правила 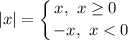 (при этом где-то нужно ноль модуля включить):
(при этом где-то нужно ноль модуля включить):
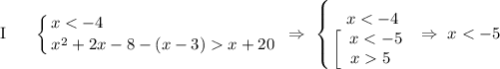
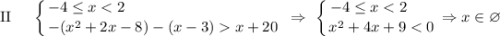
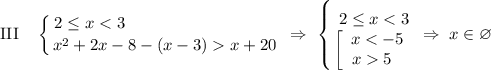

ответ: 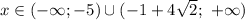

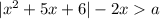
Анализируем: решение квадратного неравенства только вида 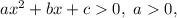 может содержать промежуток
может содержать промежуток 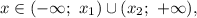 где
где 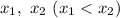 — корни квадратного уравнения
— корни квадратного уравнения 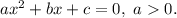
Раскроем модуль. Для этого воспользуемся правилом: 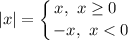
1) Пусть 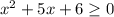
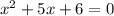
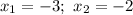 — абсциссы точек пересечения с осью абсцисс.
— абсциссы точек пересечения с осью абсцисс.
![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png)
Тогда 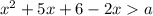
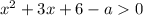
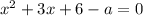
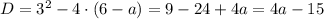
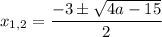
Решением исходного неравенства будет 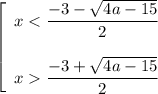
Следовательно, зная интервал 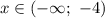 , определим значение параметра
, определим значение параметра  :
:
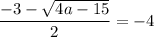
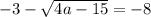
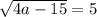
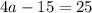
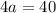
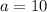
Таким образом, 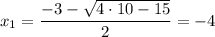 и
и 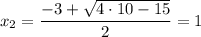
Решение: 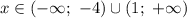
При пересечении условия модуля ![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png) получаем окончательное решение:
получаем окончательное решение: 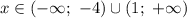 при
при 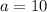
2) Если 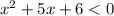 , то получаем
, то получаем 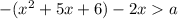 с отрицательным коэффициентом перед
с отрицательным коэффициентом перед 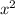 : это означает, что решением квадратного неравенства вида
: это означает, что решением квадратного неравенства вида 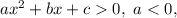 будет промежуток
будет промежуток 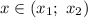 , где
, где 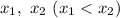 — корни квадратного уравнения
— корни квадратного уравнения 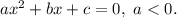 Этот случай нас не устраивает.
Этот случай нас не устраивает.
ответ: 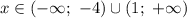 при
при 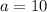
3х + 7у = - 1
Решение сложения
28х - 7у = 63
28х + 3х - 7у + 7у = 63 - 1
31х = 62
Х = 2
4•2 - у = 9
у = 8 - 9
у = - 1
ответ ( 2 ; - 1 )