а)
При -2<x≤2, графиком функции f(x) будет y=3-x². Это парабола, ветви направлены вниз, координата вершины (0;3). Найдём точки пересечения с осями координат:
x=0 ⇒ y=3-0²=3; (0;3)
y=0 ⇒ 3-x²=0; x²=3; x=±√3; (-√3;0), (√3;0).
Всё, что мы нашли находится в указанном промежутке. 3-(-2)²=3-2² - ординаты границ промежутка совпадают, период равен 4 ⇒ 2-4 = -2, поэтому график функции f(x) будет непрерывным. Таблицу точек для y=3-x² и график функции смотри в приложении.
б)
Нули для y=3-x² мы знаем, для f(x) будут такие же нули, но есть ещё период, поэтому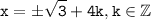 
- ответ.
в)
Определим по графику.
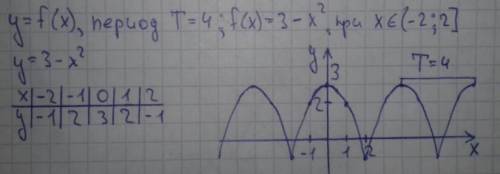
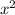+5x+4)(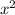+5x+6)=5040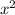+5x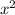+5x = t
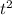+ 10t + 24 = 5040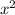+5x = 66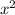+5x = -76
Как решать неравенства
1)приравниваем данное выражение(уравнение) к нулю
2)дальше решаем это уравнение
3)получается корни (точки)
4)строим луч на нем обозначает точку(точки) если несколько ,то сначала меньшее число пишем слева,потом большее
5)определяем знак больше большего числа(например больший корень 8,значит берем х=9,и подставляем в данное уравнение
Если положительное число то ставим +,а дальше чередуем +,-,+ или -,+,-
6)смотрим по неравенству какой ответ надо выбирать
Если в неравенстве >,то где стоит +,если<,то где стоит минус