Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
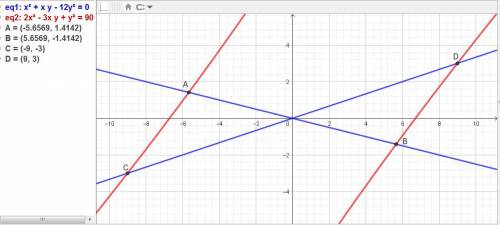
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3
h=9