Объяснение:
6) приведение к общему знаменателю (к 20 в данном случае)
8) несколько решений, 1. посчитать числа под корнем, а потом убрать корень: 2. убрать корень, сократив тем самым степени над числами (например под корнем7^2=7)
9) умножаешь все дроби на 12, затем знаменатель можно откинуть и решать как простое уравнение
13) простое раскрытие скобок, в первой по формуле (a+b)^2=(a^2+2ab+b^2), во второй простое перемножение Х на внутренности скобки (не забудь, что т.к. перед скобкой минус знак внутри скобки поменяется)
15) перенос всех Х в одну часть неравенства, цифр в другую. далее решение как у простейшего линейного уравнения
Расстояние от точки А(1/65) до точки С(1/66):
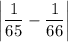
Расстояние от точки В(1/67) до точки С(1/66):
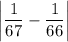
Найдем, какая из этих величин больше. Для этого сравним числа:
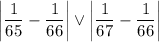
Раскроем модули, воспользовавшись правилом: из двух дробей с одинаковым числителем больше та, в которой меньше знаменатель:
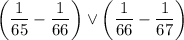
Перенесем слагаемые из одной части в другую со сменой знака:
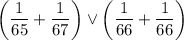
Сложим дроби:
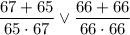
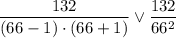
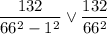
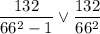
Итак, числители двух дробей одинаковы, а знаменатель первой дроби меньше знаменателя второй дроби. Это говорит о том, что первая дробь больше второй.
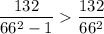
Таким образом, для исходных величин верно соотношение:
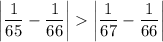
Значит, точка А расположена дальше от точки С, чем точка В.
ответ: А
функция непрерывна на (-∞; +∞)у'=(2-3x2-x3)' = - 6x - 3x2y'=0; -3x(2+x)=0; x1=0, x2=-2 - критические точки.
4. y'(x) __ + _ знаки производной
–∞ -20 +∞
y(x) убывает ↓ возрастает ↑ убывает ↓
x=-2 – точка минимума, х=0 – точка максимума
5. у(-2)= 2– 3(-2)2-(-2)3 = -2 минимум функции в точке (-2,-2)
y(0) = 2-0-0=2 максимум функции в точке (0,2)
6. Найдем нули функции: 2-3х2-х3=2-2х2-х2-х3=2(1-х2) - х2(1+х) = (1+х)(2-2х-х2) = 0,
т.о. х1=-1, х2=-1-√3 ≈ -2.7, х3=-1+√3 ≈ 0.7 .
Точки х1, х2, х3 - точки пересечения графика функции с осью OX.
7. Нанесем на плоскость полученные точки (х1,0); (х2,0), (х3,0) и точки (-2,-2), (0,2), а также используя информацию о промежутках убывания и возрастания, строим график.