Распишем цифры разрядов x, y, 4 искомого десятичного числа как:
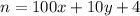
"Зачеркнём последнюю цифру", получив двузначное число:
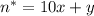
Соотношение между ними ("число уменьшится на 274"):
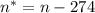
Преобразуем:
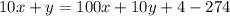
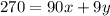
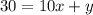
Цифра первого разряда (y) как функция цифры второго разряда (x):
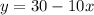
У этого уравнения бесконечное множество решений. Однако, поскольку это цифра, то имеем ограничения:
x, y - натуральные числа или 0 (цифры),
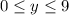 ,
,
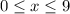 .
.
То есть:
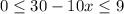
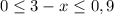
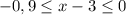
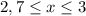
Единственным решением для целых x в заданном промежутке будет число (цифра!) 3.
Тогда y будет: y = 30 - 10*3 = 0.
Итак, ответ:
1) 1-sin²a = cos²a sin²a+cos²a. по основному тригонометрическому тождеству
следовательно √(1-sin²a)=√cos²a =| cos(a) | (по модулю)
поскольку в данном интервале cos(a) положительный => модуль можно убрать.
ответ: cos(a)
2) ctg(a) = cos(a)/sin(a)
1 + ctg²(a) = 1 + cos²(a)/sin²(a) = (sin²a+cos²a)/sin²a = 1/sin²a (sin²a+cos²a =1
по основному тригонометрическому тождеству)
√1+ctg²a = √(1/sin²a) = | 1/sin(a) |
так как на данном промежутке sin(a) отрицательный => | 1/sin(a) | = - 1/sin(a)
ответ: -1/sin(a).
x^3+2x^2 -x(x^2+2x+1)=5x+9
x^3+2x^2-x^3-2×^2-×=5×+9
-×=5×+9
-×-5×=9
-6×=9
×=-9/6
×=-3/2