1. Подкоренное выражение неотрицательно, знаменатель не равен 0
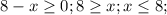
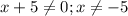
обьединяя ![D(y)=(-\infty;-5) \cup (-5;8]](/tpl/images/0033/6568/ccdfe.png)
2. Область определения - множество всех действительных чисел, x є R
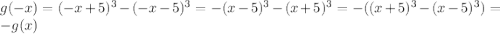
по определению функция g(x) нечетная
3. 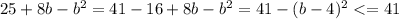 , причем равенство достигается при b=4
, причем равенство достигается при b=4
(так как квадрат любого выражения неотрицателен)
4. График во вложении
при x>=0 график имеет вид y=x^2-8x+13 вершина параболы (4;-3)
при x<0 график имеет вид y=x^2+8x+13 вершина параболы (-4;-3)
5. 2х-1=0
х=0.5 - вертикальная асимптота
ищем наклонные асимптоты
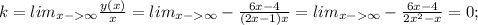
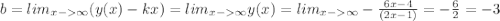
значит наклонная будет одновременно горизонтальной асимптотой и равна y=-3
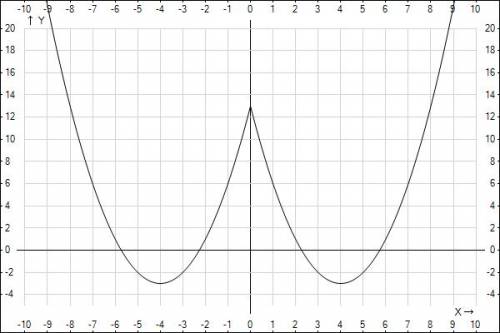
6. График во вложении
Область определения D(y)=R
Область значений функций 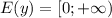
Функция четная, непериодичная
Функция положительная на R/{-2;2}
Нули функции х1=-2, х2=2
Функция убывает на 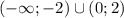
Функция возростает на 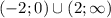
х=-2 и х=2 - точки локального минимума (y(-2)=y(2)=0)
x=0 - точка локального максимума (y(0)=4)
Асимптот функция не имеет
Т.к. нам нужно найти такое а, чтобы сумма квадратов этих чисел была наименьшей, то рассмотрим следующую функцию:
Графиком данной функции является парабола, ветви её направлены вверх, наименьшее значение она будет принимать в вершине:
Значит, a = 32.
И значит, что оба числа равны 32.
ответ: 64 = 32 + 32.