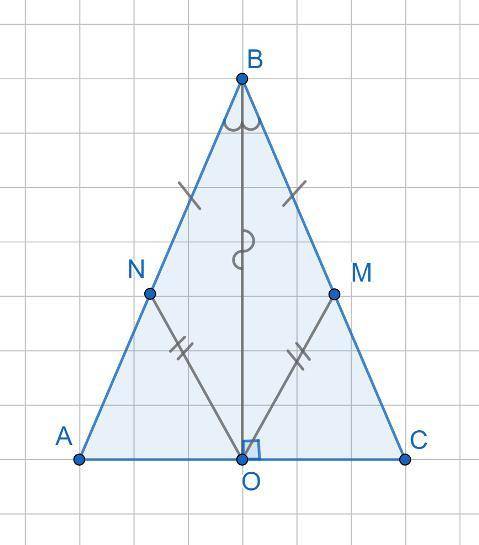
Дано: ΔABC равнобедренный; AB = BC; BO высота; BN = BM.
Доказать: NO = MO.
Доказательство:
ΔBNO = ΔBMO по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
BN = BM по условию;
BO общая сторона;
∠NBO = MBO, т.к. высота в равнобедренном треугольнике является медианой и биссектрисой. Высота BO является биссектрисой ∠NBM, т.е. делит его на на два равных угла.
Из равенства треугольников следует равенство соответствующих сторон. NO = MO, что и требовалось доказать.
Рисунок в приложении.
х ( км/ч ) - скорость первого поезда.
y ( км/ч ) - скорость второго поезда.
10х ( км ) - расстояние, которое проедет первый поезд за 10 ч.
10y ( км ) - расстояние, которое проедет второй поезд за 10 ч.
10х+10y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем первое уравнение: 10х+10у=650
8 ч + 4 ч 20 мин = 12 ч 20 мин
12 ч 20 мин =12 20\60ч=740\60ч
740\60х(км) расстояние которое проедет первый поезд за 12 ч 20 мин
8y ( км ) - расстояние, которое проедет второй поезд за 8 ч.
740\60 х + 8y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем второе уравнение: 740\60х+8у=650
получаем систему:(см.влож)
ответ: первый поезд проходит 30 км/ч, второй 35 км/ч.

9х=180
х=20
Угол 1 равен 7*20=140
Угол 2 равен 20*2=40