1,75
Объяснение:
S = x1(1-x2) + x2(1-x3) + x3(1-x4) + x4(1-x5) + x5(1-x6) + x6(1-x7) + x7(1-x1)
При условии: x1; x2; x3; x4; x5; x6; x7 ∈ [0; 1]
Очевидно, что при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0 будет S = 0
Точно также, при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 1 будет S = 0
Так как выражение симметрично относительно переменных, то любую переменную можно заменить на любую другую.
Это значит, что максимум будет достигнут при равных значениях всех переменных.
Сумма будет максимальной при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0,5
S = 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 =
= 0,25*7 = 1,75
В решении.
Объяснение:
1. Дана функция у = 8х - 3;
а) х = 10; у = ?
Подставить в уравнение значение х и вычислить значение у:
у = 8 * 10 - 3 = 80 - 3 = 77;
у = 77;
При х = 10 у = 77;
б) у = 12; х = ?
Подставить в уравнение значение у и вычислить значение х:
8х - 3 = 12
8х = 12 + 3
8х = 15
х = 15/8 (деление)
х = 1,875;
у = 12 при х = 1,875;
в) А(-0,1; -3,8); В(2,5; 1,6);
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
А(-0,1; -3,8);
-3,8 = 8 * (-0,1) - 3 = -0,8 - 3
-3,8 = -3,8, проходит;
В(2,5; 16)
16 = 8 * 2,5 - 3 = 17
16 ≠ 17, не проходит.
2.
а) х - одна сторона прямоугольника;
1,2 - другая сторона;
S прямоуг. = 1,2х - формула;
б) S прямоуг. = 1,2 * 2,7 = 3,24 (см²).
3.
Формула движения: S=v*t
S - расстояние v - скорость t – время
S = 145 - 45t - формула;
20 минут = 1/3 часа;
S = 145 - 45 * 1/3 = 145 - 15 = 130
S = 130 (км) - осталось проехать после 20 минут в пути.
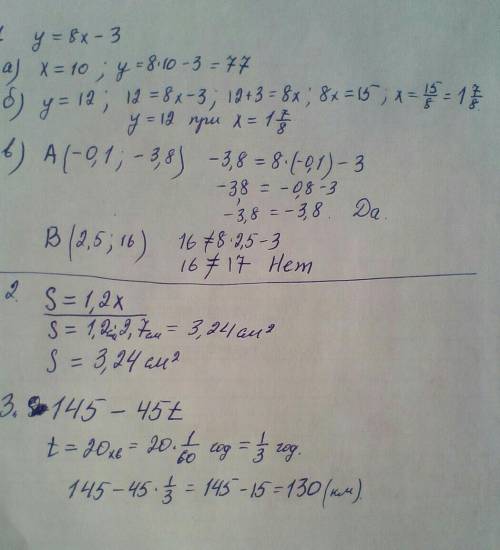
кор. 4 ст (x+8) – кор. 4 (x-8) = 2
u^4=x+8 (1)
v^4=x-8 (2)
Тогда
u-v=2
C другой стороны вычтем из (1) (2), получим
u^4 –v^4 = 16
Получаем систему
u-v=2
u^4 –v^4 = 16
Из 1-го уравнения определим u
u = v+2
Подставим во второе уравнение
(v+2)^4-v^4=16
(-v^4-16) + (v^4+8v^3+24v^2+32v+16)=0
8v^3+24v^2+32v=0
v(8v^2+24v+32)=0
Имеем,
v=0
и
8v^2+24v+32=0
v^2+3v+4=0
D=3^2-4-4*1*4=-7 < 0 – нет решений
То есть имеем одно решение v=0, тогда u = v+2=2
u^4=x+8 или x+8=2^4=16, откуда x=8