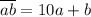
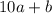 , или само число в 2 раза больше произведения ab :
, или само число в 2 раза больше произведения ab : 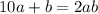 .
.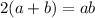 .
.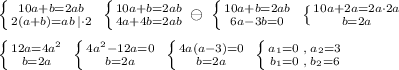
В решении.
Объяснение:
Решить уравнение:
1/(х - 4)² - 7/(х - 4) + 10 = 0
Умножить все части уравнения на (х - 4)², чтобы избавиться от дробного выражения:
1 - 7*(х - 4) + 10*(х - 4)² = 0
Разложить квадрат разности по формуле:
1 - 7*(х - 4) + 10*(х² - 8х + 16) = 0
Раскрыть скобки:
1 - 7х + 28 + 10х² - 80х + 160 = 0
Привести подобные:
10х² - 87х + 189 = 0, квадратное уравнение, ищем корни:
ОДЗ: х ≠ 4;
D=b²-4ac = 7569 - 7560 = 9 √D=3
х₁=(-b-√D)/2a
х₁=(87-3)/20
х₁=84/20
х₁=4,2;
х₂=(-b+√D)/2a
х₂=(87+3)/20
х₂=90/20
х₂=4,5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
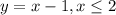

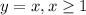
Это система.
Объяснение:
Разделим график на 3 промежутка, где функция будет либо только возрастать, либо только убывать, либо быть постоянной.
Самый простой ограничить линейные функции - ограничить область определения при неравенств.
1) Первый кусочек графика слева - y = x - 1 (-1 потому что пересекает ось Oy в данной точке), но нам ее нужно ограничить, так как в данном виде она не ограничена. x <= -2. Остальные значения x не будут удовлетворять неравенству и функция не будет определена при данных значениях.
2) Это прямая y = 1, но существует она на промежутке от -2 до 1 (по оси Ox). Тоже можно задать неравенством -2 =< x =< 1.
3) Это линейная функция y = x, однако существует она только при x >= 1
2x*y=x+10y (1)
2(x+y)=x*y (2)
(2) --->(1)
4x+4y=x+10y ⇒ 3x=6y ⇒ x=2y
Подставим вместо x в (2), получаем
2(3y)=2y² ⇒ 2y²-6y=0 ⇒ 2y(y-3)=0 ⇒ y=0 (не подходит, потому что число двузначное, а значит кол-во десятков ≥1) и y=3; x=6
То есть число 36 ответ: А)