ответ: \frac{4x^4-4x^3+x^2}{-2x^2+5x-2}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0
ОДЗ:
-2x^2+5x-2\neq0\\ 2x^2-5x+2\neq0\\ D=25-16=9; \sqrt {D}=3 x_{1/2}\neq0 x_1\neq \frac{1}{2}; \ \ x_2\neq2
-2x^2+5x-2=-(x-2)(2x-1)=(2-x)(2x-1)
\frac{x^2(4x^2-4x+1)}{(2-x)(2x-1)}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0 \frac{x^2(2x-1)^2}{(2-x)(2x-1)}+ \frac{2x^3-7x^2+5x+1}{x-2}\leqslant0 \frac{2x^3-7x^2+5x+1}{x-2}- \frac{x^2(2x-1)}{x-2}\leqslant0 \frac{2x^3-7x^2+5x+1-2x^3+x^2}{x-2}\leqslant0 -6x^2+5x+1\leqslant0 6x^2-5x+1=0\\ D=25+24=49; \ \sqrt D=7 x_{1/2}= \frac{5\pm7}{12} x_1=- \frac{1}{6};\ \ x_2=1
__+__- \frac{1}{6} __-__ \frac{1}{2} __-__1__+__2__-__
ответ: x\in [- \frac{1}{6}; \frac{1}{2})\bigcup (\frac{1 }{2};1]\bigcup(2;+\infty)
Объяснение:
Перепишем векторное уравнение в матричном виде
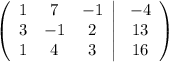
Проверим создают ли заданные векторы базис. Для этого найдем определитель матрицы
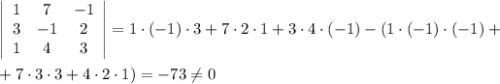
Поскольку определитель матрицы не равен нулю, то данная система векторов является базисом.
От второй строки отнимем первую строку, умноженной на 3 и от третьей строки отнимем первую строку
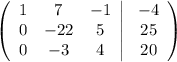
От первой строки отнимем вторую строку , умноженной на (-7/22). Сложим третью строку и вторую строку, умноженной на 3
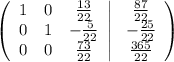
Заранее поделим третью строку на 73/22. Далее от первой строки отнимем третью строку, умноженной на 13/22; сложим вторую строку и третью строку, умноженной на 5/22

Разложение: 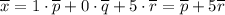
Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка.
.. отрезок имеет начало и конец. ( эти точки и есть начало и конец) .о. О— середина отрезка. делит отрезок пополам.