Если прямая касается параболы, то коэффициент a можно рассчитать как минимум 3мя разными
1)Дискриминант
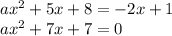
-----
Если прямая касается параболы тогда дискриминант этого уравнения будет равняться нулю.
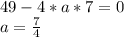
ответ 7/4
2)Теорема виета
Не сильно отличается от первого:
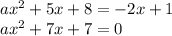
если прямая касается параболы, тогда квадратный трехчлен имеет всего один корень, тогда по т. виета:
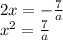
-------------
из 1:
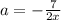
подставим в 2:
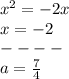
-------------
ответ 7/4 (менее быстрый метод но зато нам сразу будет известна точка касания)
3)Производная
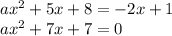
если прямая касается параболы, тогда значение производной прямой в точке касания равно значению производной параболы в точке касания:
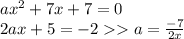
подставим в первое:
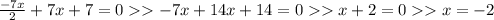
a=7/4
ответ 7/4 (Опять же не самый быстрый но зато мы сразу узнаем координаты касания)
Відповідь:
Пояснення:
Нехай швидкість другого мотоцикліста х км/ год, тоді швидкість першого (х-8) км/год. Тоді перший мотоцикліст їхав (240/х-8) год, а другий мотоцикліст їхав (240/х) год. Так як перший прибув у пункт призначення на 1 год пізніше (відповідно він їхав довше), то маємо рівняння:
240/(х-8) - 240/х = 1
240/(х-8) - 240/х - 1=0
Спільний знаменник х(х-8)
(240х - 240(х-8) - х(х-8))/(х(х-8))
(240 х - 240х + 1920-х^2 + 8х)/(х(х-8))
(- х^2+8х + 1920)/(х(х-8))
Маємо систему:
- х^2+8х + 1920=0
х(х-8) не дорівнює 0
Виписуємо перше рівняння
- х^2+8х + 1920=0
Д=7744
х1=-40
х2=48
Повертаємось до системи
х1 = -40, х2 = 48
х не дор. 0, х не дор 8
Число -40 не задовольняє умову задачі.
Отже Швидкість другого мотоцикліста 48 км/год, а швидкість першого 40 км/ год.
21y+15x=0,5 15x+21y=0,5 |×(-2) -30x-42y=-1
Суммируем эти уравнения:
-69y=23
y=-1/3 ⇒
10x-9*(-1/3)=8
10x+3=8
10x=5
x=1/2.
ответ: x=1/2 y=-1/3.