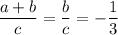Question

Если множеством решений неравентсва ax^2+bx+c> 0 является интервал (3; +беск), то чему равно (a+b)/c? с объяснением

Answer 1

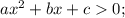Вообще неравенство $ax^2+bx+c0;$ имеет либо два промежутка с  бесконечностями на краях, либо один промежуток без бесконечностей, либо x∈R, если дискриминант отрицательный, а ветви вверх направлены, либо не имеет решений, если дискриминант неположительный (при D=0 парабола касается оси ОХ, но неравенство строгое). А здесь промежуток как при решении линейного неравенства.

А оно может быть так, если a=0

Тогда имеем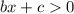 $bx+c0$

При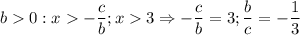 $$b0: x-\frac{c}{b} ; x3 \Rightarrow -\frac{c}{b}=3; \frac{b}{c}=-\frac{1}{3}$

А вот при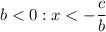 $$b$, это не годится.

Учитывая, что а=0, $$\frac{a+b}{c}=\frac{b}{c}=-\frac{1}{3}$