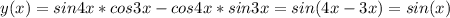
есть 
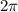
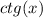равен 
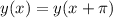
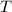- искомый период, тогда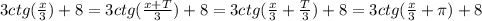
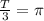
относительно оси OX на 8 единиц вверх, также не влияя на период
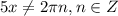
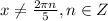
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
1)Найдите девятый член последовательности
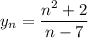
2) Найдите пятый член последовательности заданной рекуррентным у1 = ½, yₙ=2*y₍ₙ₋₁₎
y₂=2*1/2=1; y₃=2*1=2; y₄=2*2=4; y₅=2*4=8
3) Подберите формулу n- го члена последовательности - 2/2; 4/5; - 6/8; 8/11; -10/14;
проверка:
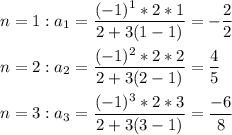
4) Сколько членов последовательности 3, 6, 9, 12,….меньше числа 95
аₙ=а₁+3(n-1)
aₙ<95
a₁+3(n-1)<95
3+3n-3<95
3n<95
n<31.(6)
n=31
проверим: a₃₁=3+3(31-1)=3+3*30=93
Значит 31 член меньше 95
5) у₁ = 2, у₂ = 1, уₙ = 2y₍ₙ₋₂₎+3y₍ₙ₋₁₎ (n = 3,4,5,…).Найдите n, если известно, что уₙ = 83.
тут можно просто решить находя слены этой последовательности
y₁=2
y₂=1
y₃=2*2+3*1=4+3=7
y₄=2*1+3*7=2+21=23
y₅=2*7+3*23=14+69=83
N=5
решение представлено на фото
Объяснение: