~31,9
Объяснение:
3x+12y+34y
x=0,4
y=2\3
Переведём значение X в обыкновенную дробь:
0,4 = 4\10.
Сложем подобные слогаемые:
12y+34y=46y
Запишем упрощённое выражение:
3x+46y
Вместо X подставим 4\10, а вместо y 2\3 в выражение.
3*4\10+46*2\3
Решим его по действиям:
1) Умножем 3 на 4\10
3*4\10=12\10
2) Умножем 46 на 2\3
46*2\3=92\3
Теперь получилось:
12\10+92\3
Складываем:
Приводим к общему знаменателю 10*3=30 - общий знаменатель
Общий множитель первой дроби 3
Второй дроби 10
Домножаем числители на них:
12*3=36
92*10=920
Получилось:
36\30+920\30
Теперь можно сложить:
920+36=956\30
Переведём в десятичную
956\30=31,9
Объяснение:
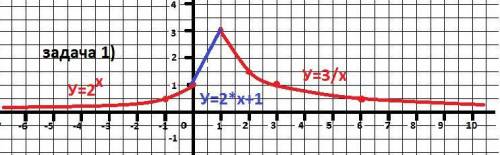
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
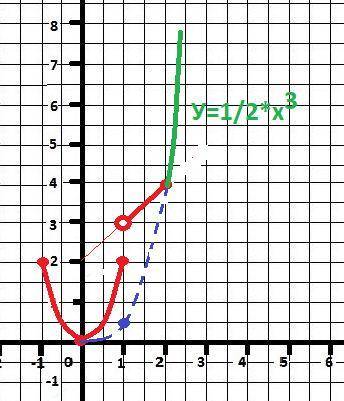
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.
х³ - 3·х²·4 + 3·х·4² - 4³ - х³ - 39х = - 54 - 10х²
- 12х² + 48х - 64 - 39х + 54 + 10х² = 0
- 2х² + 9х - 10 = 0
2х² - 9х + 10 = 0
D = b² - 4ac
D = 81 - 4·2·10 = 81 - 80 = 1
√D = √1 = 1
x₁ =(9 - 1)/4 = 2
x₂ = (9 + 1)/4 = 10/4 = 2,5