1) Доказать:
а^2 - 3а > 5а - 20
Доказательство:
Оценим разность:
(а^2 - 3а) - (5а - 20) = а^2 - 3а - 5а + 20 = а^2 - 8а + 20 = а^2 - 8а + 16 + 4 = (а-4)^2 + 4.
Так как (а-4)^2 ≥ 0 при всех действительных а, то (а-4)^2 + 4 ≥ 4, т.е.
(а^2 - 3а) - (5а - 20) > 0, по определению
а^2 - 3а > 5а - 20, ч.т.д.
2) Доказать:
28а - 32 ≤ 7а^2 - 4
Доказательство:
Оценим разность:
(28а - 32) - (7а^2 - 4) = 28а - 32 - 7а^2 + 4 = -7а^2 + 28а - 28 = -7•(а^2 - 4а + 4) = -7•(а-2)^2.
Так как (а-2)^2 ≥ 0 при всех действительных а, то
-7•(а-2)^2 ≤ 0 при всех действительных а.
Получили, что
(28а - 32) - (7а^2 - 4) ≤ 0, тогда по определению
28а - 32 ≤ 7а^2 - 4, ч.т.д.
№13 - 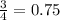
№14 - 
№15 - 
Объяснение:
По определению производной:
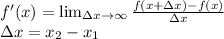
Заметим, что  - это отношение
- это отношение  , т.е. тангенс угла наклона касательной в точке
, т.е. тангенс угла наклона касательной в точке 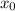 .
.
Тогда совершенно очевидно, как решать подобного рода задачи:
анализируем только касательнуюнаходим точку, где касательная проходит через угол клеточкинаходим тангенс угла, образованного осью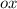 и касательной.
и касательной.На примере задания №14:
смотрим на прямуювидим, что она проходит через точку находим тангенс (делим противолежащий катет на прилежащий, в данном случае - высоту на длину)ответ: 2
находим тангенс (делим противолежащий катет на прилежащий, в данном случае - высоту на длину)ответ: 2
№13 - 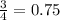
№14 - 
№15 - 
Объяснение:
По определению производной:
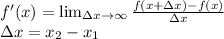
Заметим, что  - это отношение
- это отношение  , т.е. тангенс угла наклона касательной в точке
, т.е. тангенс угла наклона касательной в точке 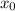 .
.
Тогда совершенно очевидно, как решать подобного рода задачи:
анализируем только касательнуюнаходим точку, где касательная проходит через угол клеточкинаходим тангенс угла, образованного осью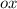 и касательной.
и касательной.На примере задания №14:
смотрим на прямуювидим, что она проходит через точку находим тангенс (делим противолежащий катет на прилежащий, в данном случае - высоту на длину)ответ: 2
находим тангенс (делим противолежащий катет на прилежащий, в данном случае - высоту на длину)ответ: 2
В этих заданиях для меня проще выделить полный квадрат.
неравенство верно для всех а.
Левая часть - неотрицательно, неравенство верно для всех а.