ответ:Для того, чтобы представить выражение 4x^2 + y^2 + 4xy в виде квадрата двучлена мы применим формулу сокращенного умножения квадрат суммы.
Итак, вспомним прежде всего формулу квадрат суммы:
(a + b)^2 = a^2 + 2ab + b^2.
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Но прежде чем применить формулу преобразуем выражение к виду:
4x^2 + y^2 + 4xy = 4x^2 + 4xy + y^2 = (2x)^2 + 2 * 2x * y + y^2 = (2x + y)^2.
Объяснение:
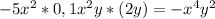; коэффициент - число (- 1); степень одночлена равна 6.
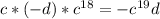; коэффициент - число (-1); степень одночлена равна 20
-2sin(x) -1 = 0
sin(x) = -1/2
x = (-1)ⁿ arcsin(-1/2) +πn, n ∈ Z
x = (-1)ⁿ⁺¹ arcsin(1/2) +πn, n ∈ Z
x = (-1)ⁿ⁺¹ π/6 +πn, n ∈ Z