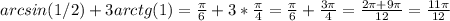
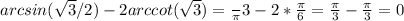
Дана функция y=x^4-2x^3+3.
Её производная равна: y' = 4x³- 6x².
Приравняем производную нулю:
4x³- 6x² = 2x²(2х - 3) = 0.
Отсюда находим 2 критические точки (они же стационарные):
х = 0 и х = 3/2.
Они разбивают область определения функции на 3 промежутка:
(-∞; 0), (0; 3/2)) и ((3/2); +∞).
Определяем свойства полученных точек по знаку производной в найденных промежутках.
х = -1 0 1 3/2 2
y' = -10 0 -2 0 8 .
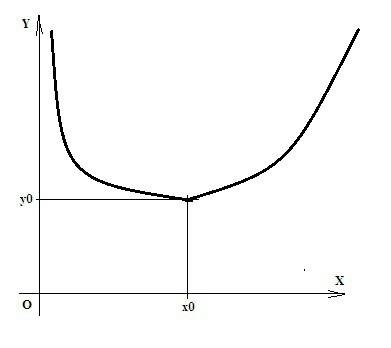
Как видим, есть только одна точка экстремума-это минимум функции в точке х = 3/2.
вроде так.