Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Объяснение:
y = - x⁴ + 8x² - 16
y' = - 4x³ + 16x
y' = 0
- 4x³ + 16x = 0
4x(x² - 4) = 0
x = 0, x² - 4 = 0
(x - 2)(x + 2) = 0
x = 2 x = - 2
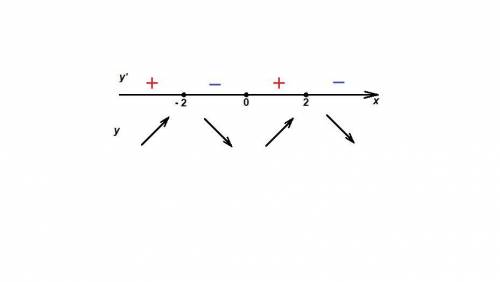
Отметим точки на координатной прямой и определим знаки производной на получившихся интервалах (знаки чередуются, справа минус), см. рисунок.
Если на промежутке производная положительна, то функция возрастает, если отрицательна - убывает.
Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Найти первый положительный член арифметической прогрессии -10,2; -8,3; ...
Арифметическая прогрессия - это последовательность чисел, каждый член которой, начиная со второго, равен предыдущему, увеличенному на одно и тоже число (разность арифметической прогрессии, обозначается d).
По условию а₁ = -10,2, a₂ = -8,3, тогда d = a₂ - a₁ = -8,3 - (-10,2) = -8,3 + 10,2 = 10,2 - 8,3 = 1,9.
an = a₁ + d(n - 1) - формула n-го члена
По условию аn > 0, поэтому решим получившееся неравенство
-10,2 + 1,9(n - 1) > 0,
-10,2 + 1,9n - 1,9 > 0,
1,9n - 12,1 > 0,
1,9n > 12,1,
19n > 121,
n > 121/19 = 6 целых 7/19.
Значит, n = 7.
Найдем а₇:
а₇ = -10,2 + 1,9(7 - 1) = -10,2 + 1,9 · 6 = -10,2 + 11,4 = 11,4 - 10,2 = 1,2.
ответ: 1,2.