Кол-во таких чисел=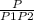 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 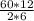 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
1) Находим производную
f`(x)=10x-4
2)приравниваем её к нулю
10x-4=0
x=0,4
3) рисуем ось Ох, отмечаем на ней точку с координатой 0,4
4)выбираем точку до 0,4(пусть будет 0) и точку после 0,4( пусть будет 1)
решаем 10x-4, подставляя вместо х значения (0 и 1)
При х=0 10х-4=-4(число отрицательное)
При х=1 10х-4=6(число положительное).
По правилу те значения х, в которых производная больше нуля являются промежутками возрастания функции, те значения х, в которых меньше нуля, являются промежутками убывания.
Функция убывает на промежутке (-бесконечность;0,4)
3) (a+5)(a^2+25)(a-5)=(a^2-25)(a^2+25)=a^4-625
4) 8x^2+16x+8=8(x+1)(x+1)
8x^2+16x+8=0| разделим обе части уравнения на 8
x^2+2x+1=0
Так как коэффициент при x^2 равен 1, то корни можем найти по теореме Виета:
х1=-1, х2=-1